题目内容
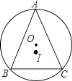
【题目】如图，
是
的直径，点
在上，
，垂足为
，弧
等于弧
，
分别交
、
于点
、
．
判断
的形状，并说明理由；
若点
和点在的两侧，、的延长线交于点，的延长线交于点，其余条件不变，中的结论还成立吗？请说明理由．
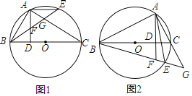
【答案】（1）等腰三角形，理由见解析；（2）成立；理由见解析
【解析】
（1）首先根据圆周角定理及垂直的定义得到∠BAD+∠CAD=90°，∠C+∠CAD=90°，从而得到∠BAD=∠C，然后利用等弧对等角等知识得到AF=BF，从而证得FA=FG，判定等腰三角形；
（2）成立，证明方法同（1）．
解：
等腰三角形；
∵
为直径，
，
∴
，
，
∴
，
∵
，
∴
，
∴
，
∴
，
∵，
，
∴
，
∴
，
∴
是等腰三角形；
成立；
∵为直径，，
∴，，
∴，
∵，
∴，
∴，
∴，
∵，，
∴，
∴，
∴是等腰三角形．
练习册系列答案
灵星计算小达人系列答案
相关题目
