题目内容
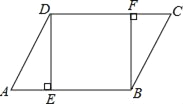
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 的延长线上,
的延长线上,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
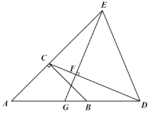
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() .求证:
.求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)在△CDE中根据等腰三角形的性质和三角形内角和定理得到∠ECD的度数.在△ACD中,根据三角形外角的性质即可得出结论;
(2)在△CDE中,根据等腰三角形的性质得到∠ECD=∠CED,进而得到∠ECD+∠CDB=90°.由∠ECD+∠DCB=90°,得到∠DCB=∠BDC.由∠DCB+∠BDC=∠ABC=45°,得到∠DCB=∠BDC=22.5°,得到∠ECD=∠CED=67.5°,得到∠EDC=45°.由EF⊥DC于点F,得到∠DEF=∠EDC=45°,即有EF=DF,∠EDG=∠EGD=67.5°,根据等角对等边得到EG=ED,等量代换得到EG=DC,即可得到结论.
∵等腰![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
又∵CD=DE,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)∵CD=DE,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目