Question

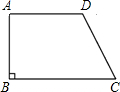
如图，在直角梯形ABCD中，∠B=90°，AD∥BC，且AD=4cm，AB=6cm，DC=10cm．若动点P从A点出发，以每秒4cm的速度沿线段AD、DC向C点运动；动点Q从C点出发以每秒5cm的速度沿CB向B点运动．当Q点到达B点时，动点P、Q同时停止运动．设点P、Q同时出发，并运动了t秒，
（1）直角梯形ABCD的面积为______cm²；
（2）当t=______秒时，四边形PQCD成为平行四边形？
（3）当t=______秒时，AQ=DC；
（4）是否存在t，使得P点在线段DC上且PQ⊥DC？若存在，求出此时t的值；若不存在，说明理由．

Answer 1

（1）作DM⊥BC于点M．则四边形ABMD是平行四边形
∴DM=AB=6cm．
在直角△CDM中，CM=

CD2-DM2

=8cm
∴BC=BM+CM=4+8=12cm
∴直角梯形ABCD的面积为

1

2

（AD+BC）•AB=48cm²；

（2）当PD=CQ时，四边形PQCD成为平行四边形
即4-4t=5t
解得t=

4

9

；

（3）BQ=12-5t
在直角△ABQ中，AB²+BQ²=AQ²
即6²+（12-5t）²=10²
解得t=

4

5

；

（4）存在，t=

7

4

．
连接QD，则CP=14-4t，CQ=5t
若QP⊥CD，则2S_△DQC=CQ×AB=CD×QP
得QP=3t
在Rt△QPC中
QP²+PC²=CQ²，即（3t）²+（14-4t）²=（5t）²
解之得t=

7

4

求得BC=12
CP=14-4t=7＜10
CQ=5t=

35

4

＜12
所以，存在t，使得P点在线段DC上，且PQ⊥DC．