题目内容
【题目】如图,点![]() ,
,![]() 都在双曲线
都在双曲线![]() (
(![]() )上,
)上,![]() 分别是
分别是![]() 轴,
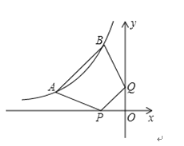
轴,![]() 轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的表达式为( )
轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的表达式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
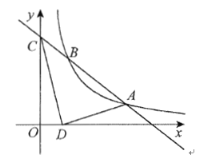
先求出A、B的坐标,如下图,分别作点A、B关于x轴、y轴的对称点C、D,连接CD与x轴、y轴的交点即为点P、Q,从而求出PQ所在直线解析式.
∵点![]() ,
,![]() 都在双曲线
都在双曲线![]() 上
上
∴A(-3,1),B(-1,3)
如下图,分别作点A、B关于x轴、y轴的对称点C、D,连接CD与x轴、y轴交于点M、N

则点C(-3,-1),D(1,3)
∵四边形ABQP的周长=AB+BQ+PQ+PA
其中,AB是定值,BQ=DQ,AP=CP,PQ=PQ
如上图,当点P、Q为M、N两点时
则CP、PQ、QD三段直线共线,距离最小
∴上图中点M、N即为P、Q
则将C、D两点代入,可求得PQ所在直线解析式为:![]()
故选:C.

练习册系列答案
相关题目