题目内容
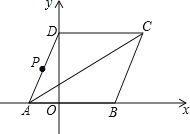
【题目】如图所示,菱形![]() 的顶点
的顶点![]() 在
在![]() 轴上,点
轴上,点![]() 在点
在点![]() 的左侧,点
的左侧,点![]() 在
在![]() 轴的正半轴上.点
轴的正半轴上.点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,按照
出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.
秒.
(1)①点![]() 的坐标 .②求菱形
的坐标 .②求菱形![]() 的面积.
的面积.
(2)当![]() 时,问线段
时,问线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 最小,如果存在,求出
最小,如果存在,求出![]() 最小值;如果不存在,请说明理由.
最小值;如果不存在,请说明理由.
(3)若点![]() 到
到![]() 的距离是1,则点
的距离是1,则点![]() 运动的时间
运动的时间![]() 等于 .
等于 .

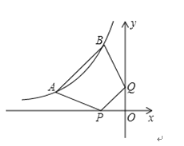
【答案】(1)①(2,0) ②![]() (2)存在;
(2)存在;![]() (3)
(3)![]()
【解析】
(1)①过点![]() 作
作![]() ,根据点C的坐标求出BF的长度,便可求出C的坐标.
,根据点C的坐标求出BF的长度,便可求出C的坐标.
②根据已知,得到![]() ,
,![]() 菱形的面积为便可计算出
菱形的面积为便可计算出
(2)作点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,则有
,则有![]()
便可找到最小值了.
(3)分四种情况进行讨论即可.
解:![]() ①
①![]()
②过点![]() 作
作![]() 垂足为
垂足为![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]()
在菱形![]() 中,
中,![]()
![]()
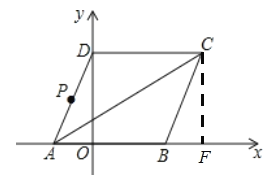
![]() 如图所示:当
如图所示:当![]() 时,
时,![]()
在菱形![]() 中,点
中,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]()
连结![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.
![]()
由![]() 易得
易得![]()
![]()
在![]() 中
中
![]()
![]()
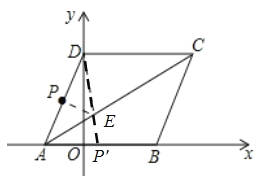
![]() 最小值为
最小值为![]()
(3)分四种情况讨论:
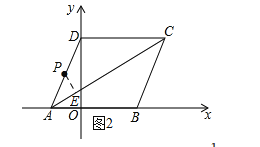
第一种,如图2所示
![]()
![]()
![]()
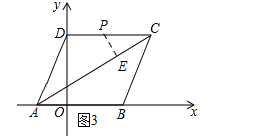
第二种如图3所示
![]()
![]()
![]()
![]()
![]()
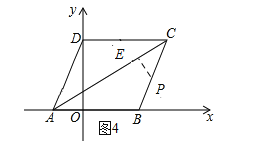
第三种情况如图4所示
同理可以得到![]()
![]()
![]()
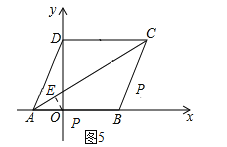
第四种情况如图5所示
同理可以得到AP=2
![]()
![]()
综上所述,满足条件的为:![]()

练习册系列答案
相关题目
【题目】为了解某种车的耗油量,我们对这种车做了试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | ······ |
剩余油量Q(L) | 50 | 44 | 38 | 32 | ······ |
(1)根据上表的数据,能用t表示Q吗?试一试;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为14L,则汽车行使了多少小时?
(4)贮满50L汽油的汽车,最多行驶几小时?