题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点,将三角形
为坐标原点,将三角形![]() 进行平移,平移后点
进行平移,平移后点![]() 的对应点分别是点
的对应点分别是点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
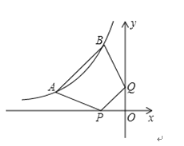
(2)若点![]() ,其中
,其中![]() . 直线
. 直线![]() 交
交![]() 轴于点
轴于点![]() ,且三角形
,且三角形![]() 的面积为1,试探究
的面积为1,试探究![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)![]() 的值为6;(2)
的值为6;(2)![]() .理由详见解析.
.理由详见解析.
【解析】
1)当a=1时,得出A、B、D、E四点的坐标,再根据平移的规律得到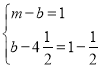 ,即可求出m的值;
,即可求出m的值;
(2)由平移的规律得出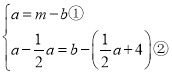 ,变形整理得到
,变形整理得到![]() ,那么CE∥x轴,根据三角形BEM的面积
,那么CE∥x轴,根据三角形BEM的面积![]() ,求出a=2,A(0,2),B(0,6),C(-2,5).根据点F与点C是对应点,得出F(0,4),求出AF=BF=2.
,求出a=2,A(0,2),B(0,6),C(-2,5).根据点F与点C是对应点,得出F(0,4),求出AF=BF=2.
解:(1)当![]() 时,
时,
由三角形![]() 平移得到三角形
平移得到三角形![]() ,
,
![]() 的对应点分别为
的对应点分别为
![]() ,
,![]()
可得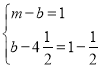 ,
,
解得![]() .
.
∴![]() 的值为6.
的值为6.
(2)由三角形![]() 平移得到三角形
平移得到三角形![]() ,
,
![]() ,
,![]() 的对应点分别为
的对应点分别为
![]() ,
,![]() .
.
可得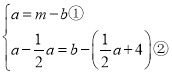 ,
,
由②得![]() ③,
③,
把③代入①,得![]() ,
,
∴![]() ,
,
∴点![]() 与点
与点![]() 的纵坐标相等,
的纵坐标相等,
∴![]() 轴,
轴,
∴点![]() ,
,
∴三角形![]() 的面积
的面积![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
又∵在平移中,点![]() 与点
与点![]() 是对应点,
是对应点,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目