题目内容
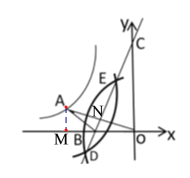
【题目】如图,点![]() 在双曲线
在双曲线![]() 上,连接
上,连接![]() ,分别以点
,分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() 两点,直线
两点,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的值为___.
的值为___.

【答案】![]()
【解析】
过点A作AM⊥x轴于点M,设AO与BC交于点N,易证![]() ,得
,得![]() ,设AM=a,可得:MO=3a,由勾股定理,列出关于a的方程,求出a的值,进而的点A的坐标,即可求解.
,设AM=a,可得:MO=3a,由勾股定理,列出关于a的方程,求出a的值,进而的点A的坐标,即可求解.
过点A作AM⊥x轴于点M,设AO与BC交于点N,
∵由作图可知:BC垂直平分AO,
∴∠AOM+∠CON=∠CON+∠DCO=90°,![]() ,
,
∴∠AOM=∠DCO,
∵∠AMO=∠BOC=90°,
∴![]() ,
,
∴![]() ,
,
设AM=a,
∴![]() ,即:MO=3a,
,即:MO=3a,
∴BM=3a-1,
∵在Rt![]() ABM中,AB2=AM2+BM2,
ABM中,AB2=AM2+BM2,
∴12=a2+(3a-1)2,解得:![]() (舍去),
(舍去),
∴AM=![]() ,MO=
,MO=![]() ,
,
∴A(-![]() ,
,![]() ),
),
∵点![]() 在双曲线
在双曲线![]() 上,
上,
∴k=(-![]() )×
)×![]() =
=![]() .
.
故答案是:![]() .
.

练习册系列答案
相关题目
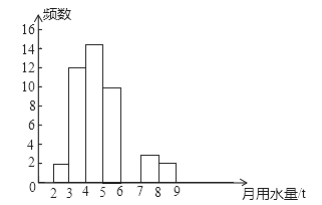
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.