题目内容
【题目】二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值2n,则m+n的值等于( )
A.0B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意可得m<0,n>0,则y的最小值为2m为负数,最大值为2n为正数.
最大值为2n分两种情况:①结合抛物线顶点纵坐标的取值范围,求出n=2.5,结合图象最小值只能由x=m时求出;②结合抛物线顶点纵坐标的取值范围,图象最大值只能由x=n求出,最小值只能由x=m求出.
二次函数y=-(x-1)2+5的大致图象如下:
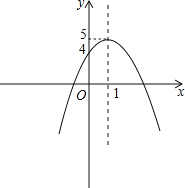 .
.
①当m<0≤x≤n<1时,当x=m时,y取最小值,即2m=-(m-1)2+5,
解得:m=-2,m=2(舍去).
当x=n时,y取最大值,即2n=-(n-1)2+5,
解得:n=2或n=-2(均不合题意,舍去);
②当m<0≤x≤1≤n时,当x=m时,y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=1时,y取最大值,即2n=-(1-1)2+5,
解得:n=2.5,
或x=n时,y取最小值,x=1时,y取最大值,
2m=-(n-1)2+5,n=2.5,
∴m=![]() ,
,
∵m<0,
∴此种情形不合题意,
所以m+n=-2+2.5=0.5.
故选:B.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目