题目内容
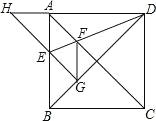
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】试题分析:∵四边形ABCD是菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABF和△CBF中,
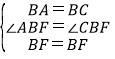 ,
,
∴△ABF≌△CBF,
∴∠BAF=∠BCF,①正确;
作EG⊥AB交AB的延长线于G,
∵AD∥BC,∠DAB=60°,
∴∠EBG=60°,
EB=BC-CE=4,
∴EG=EB×sin∠EGB=4×![]() =
=![]() ,②正确;
,②正确;
∵AB=6,CE=2,
∴S△BEF=2S△CEF,
∵AD∥BC,
∴![]() ,
,
∴S△CFD=![]() S△CFB,
S△CFB,
∴S△CDF:S△BEF=9:4,③正确;
作FH⊥CD于H,
则DH=![]() DF=2,FH=
DF=2,FH=![]() ,
,
∴tan∠DCF=![]() =
=![]() =
=![]() ,④错误,
,④错误,
故选B.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目