题目内容
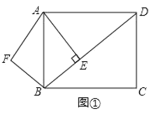
【题目】在正方形ABCD中,AB=6,连接AC,BD,P是正方形边上或对角线上一点,若PD=2AP,则AP的长为_____.
【答案】2,2![]() 或
或![]()
【解析】
根据正方形的性质得出AC⊥BD,AC=BD,OB=OA=OC=OD,AB=BC=AD=CD=6,∠ABC=90°,根据勾股定理求出AC、BD、求出OA、OB、OC、OD,画出符合的三种情况,根据勾股定理求出即可.
解:∵四边形ABCD是正方形,AB=6,
∴AC⊥BD,AC=BD,OB=OA=OC=OD,AB=BC=AD=CD=6,∠ABC=∠DAB=90°,
在Rt△ABC中,由勾股定理得:![]() ,
,
![]() .
.
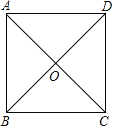
有6种情况:①点P在AD上时,
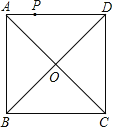
∵AD=6,PD=2AP,
∴AP=2;
②点P在AC上时,
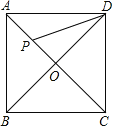
设AP=x,则DP=2x,
在Rt△DPO中,由勾股定理得:DP2=DO2+OP2,
![]() ,
,
解得:![]() (负数舍去),
(负数舍去),
即AP=![]() ;
;
③点P在AB上时,
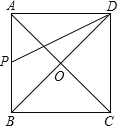
设AP=y,则DP=2y,
在Rt△APD中,由勾股定理得:AP2+AD2=DP2,
y2+62=(2y)2,
解得:y=2![]() (负数舍去),
(负数舍去),
即AP=2![]() ;
;
④当P在BC上,设BP=x,
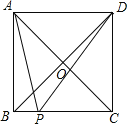
∵DP=2AP,
![]()
即x2+6x+24=0,
△=62-4×1×24<0,此方程无解,
即当点P在BC上时,不能使DP=2AP;
⑤P在DC上,
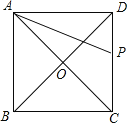
∵∠ADC=90°,
∴AP>DP,不能DP=2AP,
即当P在DC上时,不能具备DP=2AP;
⑥P在BD上时,

过P作PN⊥AD于N,过P作PM⊥AB于M,
∵四边形ABCD是正方形,
∴∠DAB=∠ANP=∠AMP=90°,
∴四边形ANPM是矩形,
∴AM=PN,AN=PM,
∵四边形ABCD是正方形,
∴∠ABD=45°,
∵∠PMB=90°,
∴∠MBP=∠MPB=45°,
∴BM=PM=AN,
同理DN=PN=AM,
设PM=BM=AN=x,则PN=DN=AM=6-x,
都不能DP=2AP,
∵DP=2AP,
∴由勾股定理得:![]() ,
,
即x2-4x+12=0,
△=(-4)2-4×1×12<0,此方程无解,
即当P在BD上时,不能DP=2AP,
故答案为2或2![]() 或
或![]() .
.