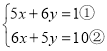Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥—ß–£ő™łń…∆įž—ßŐűľĢ£¨ľ∆Ľģ≤…ĻļA°ĘBŃĹ÷÷–ÕļŇĶńŅ’Ķų£¨“—÷™≤…Ļļ3Ő®A–ÕŅ’ĶųļÕ2Ő®B–ÕŅ’Ķų£¨–Ť∑—”√39000‘™£Ľ4Ő®A–ÕŅ’ĶųĪ»5Ő®B–ÕŅ’ĶųĶń∑—”√∂ŗ6000‘™£ģ
£®1£©«ůA–ÕŅ’ĶųļÕB–ÕŅ’Ķų√ŅŐ®łų–Ť∂ŗ…Ŕ‘™£Ľ
£®2£©»Ű—ß–£ľ∆Ľģ≤…ĻļA°ĘBŃĹ÷÷–ÕļŇŅ’ĶųĻ≤30Ő®£¨«“A–ÕŅ’ĶųĶńŐ® ż≤Ľ…Ŕ”ŕB–ÕŅ’ĶųĶń“ĽįŽ£¨ŃĹ÷÷–ÕļŇŅ’ĶųĶń≤…Ļļ◊‹∑—”√≤Ľ≥¨Ļż217000‘™£¨ł√–£Ļ≤”–ńńľł÷÷≤…Ļļ∑Ĺįł£Ņ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨≤…”√ńń“Ľ÷÷≤…Ļļ∑ĹįłŅ… Ļ◊‹∑—”√◊ÓĶÕ£¨◊ÓĶÕ∑—”√ «∂ŗ…Ŕ‘™£Ņ
°ĺīūįł°Ņ£®1£©A–ÕŅ’ĶųļÕB–ÕŅ’Ķų√ŅŐ®łų–Ť9000‘™°Ę6000‘™£Ľ£®2£©Ļ≤”–»ż÷÷≤…Ļļ∑Ĺįł£¨∑Ĺįł“Ľ£ļ≤…ĻļA–ÕŅ’Ķų10Ő®£¨B–ÕŅ’Ķų20Ő®£¨∑Ĺįł∂Ģ£ļ≤…ĻļA–ÕŅ’Ķų11Ő®£¨B–ÕŅ’Ķų19Ő®£¨įł»ż£ļ≤…ĻļA–ÕŅ’Ķų12Ő®£¨B–ÕŅ’Ķų18Ő®£Ľ£®3£©≤…ĻļA–ÕŅ’Ķų10Ő®£¨B–ÕŅ’Ķų20Ő®Ņ… Ļ◊‹∑—”√◊ÓĶÕ£¨◊ÓĶÕ∑—”√ «210000‘™£ģ
°ĺĹ‚őŲ°Ņ£®1£©łýĺ›Ő‚“‚Ņ…“‘Ń–≥ŲŌŗ”¶Ķń∑Ĺ≥Ő◊ť£¨ī”∂ÝŅ…“‘Ĺ‚īūĪĺŐ‚£Ľ
£®2£©łýĺ›Ő‚“‚Ņ…“‘Ń–≥ŲŌŗ”¶Ķń≤ĽĶ» Ĺ◊ť£¨ī”∂ÝŅ…“‘«ůĶ√”–ľł÷÷≤…Ļļ∑Ĺįł£Ľ
£®3£©łýĺ›Ő‚“‚ļÕ£®2£©÷–ĶńĹŠĻŻ£¨Ņ…“‘Ĺ‚īūĪĺŐ‚£ģ
£®1£©…ŤA–ÕŅ’ĶųļÕB–ÕŅ’Ķų√ŅŐ®łų–Ťx‘™°Ęy‘™£¨
![]() £¨Ĺ‚Ķ√£¨
£¨Ĺ‚Ķ√£¨![]() £¨
£¨
īū£ļA–ÕŅ’ĶųļÕB–ÕŅ’Ķų√ŅŐ®łų–Ť9000‘™°Ę6000‘™£Ľ
£®2£©…ŤĻļ¬ÚA–ÕŅ’ĶųaŐ®£¨‘ÚĻļ¬ÚB–ÕŅ’Ķų£®30-a£©Ő®£¨
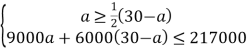 £¨
£¨
Ĺ‚Ķ√£¨10°‹a°‹12![]() £¨
£¨
°ŗa=10°Ę11°Ę12£¨Ļ≤”–»ż÷÷≤…Ļļ∑Ĺįł£¨
∑Ĺįł“Ľ£ļ≤…ĻļA–ÕŅ’Ķų10Ő®£¨B–ÕŅ’Ķų20Ő®£¨
∑Ĺįł∂Ģ£ļ≤…ĻļA–ÕŅ’Ķų11Ő®£¨B–ÕŅ’Ķų19Ő®£¨
∑Ĺįł»ż£ļ≤…ĻļA–ÕŅ’Ķų12Ő®£¨B–ÕŅ’Ķų18Ő®£Ľ
£®3£©…Ť◊‹∑—”√ő™w‘™£¨
w=9000a+6000£®30-a£©=3000a+180000£¨
°ŗĶĪa=10 Ī£¨w»°Ķ√◊Ó–°÷Ķ£¨īň Īw=210000£¨
ľī≤…ĻļA–ÕŅ’Ķų10Ő®£¨B–ÕŅ’Ķų20Ő®Ņ… Ļ◊‹∑—”√◊ÓĶÕ£¨◊ÓĶÕ∑—”√ «210000‘™£ģ