题目内容
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径作
为直径作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,直线
,直线![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
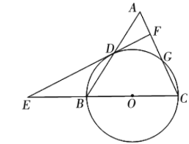
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD和CD,根据圆周角定理求出∠BDC=90°,根据等腰三角形的性质求出AD=BD,根据三角形的中位线求出OD∥AC,求出OD⊥EF,根据切线的判定得出即可;
(2)根据余角的性质得到∠ADF=∠ODC,等量代换得到∠ADF=∠OCD,根据勾股定理得到CD=12,根据三角函数的定义即可得到结论.
(1)证明:如图,连接OD,CD,
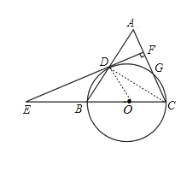
∵BC为⊙O的直径,
∴∠BDC=90°(直径所对的圆周角是90°),
即CD⊥AB,
∵AC=BC,AB=10,
∴AD=BD=5,
∵O为BC中点,
∴OD∥AC,
∵DF⊥AC,
∴∠DFC=90°,
∴∠FDO=180°-90°=90°(两直线平行,同旁内角互补),
∴OD⊥EF,
又∵OD过圆心O点,
∴直线DF是⊙O的切线;
(2)∵∠ADC=∠BDC=90°,∠ODF=90°,
∴∠ADF=∠ODC,
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADF=∠OCD(等量替换),
∵BD=5,BC=13,
∴CD=![]() = 12(勾股定理),
= 12(勾股定理),
![]() ;
;

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目