Question

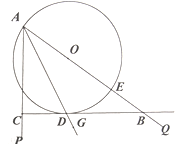
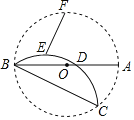
【题目】如图，AB是⊙O的直径，BC是弦，沿BC对折劣弧BC，交AB于D，点E、F分别是弧AB和弧BD的中点．若AD＝4，AB＝10，则EF＝_____．

Answer 1

【答案】2

【解析】

连接OF、设点O关于BC的对称点为O'，则O'为对折后的弧BDC的圆心，连接O'E，O'D，由垂径定理和对称的性质得出O'E⊥BD，OF⊥AB，O'E＝O'D＝OF，PB＝PD，O'E∥OF，证出四边形OFEO'是平行四边形，得出EF＝O'O，求出OP＝OB﹣PB＝2，在Rt△PO'D中，由勾股定理得出O'P＝4，O'O＝，即可得出答案．

解：连接OF、设点O关于BC的对称点为O'，则O'为对折后的弧BDC的圆心，连接O'E，O'D，如图所示：

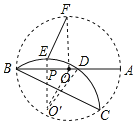
∵点E、F分别是弧AB和弧BD的中点，

∴O'E⊥BD，OF⊥AB，O'E＝O'D＝OF，

∴PB＝PD，O'E∥OF，

∴四边形OFEO'是平行四边形，

∴EF＝O'O，

∵AD＝4，AB＝10，

∴OB＝5，BD＝6，

∴PB＝PD＝3，

∴OP＝OB﹣PB＝2，

在Rt△PO'D中，O'P＝＝4，

∴O'O＝＝＝2，

∴EF＝2；

故答案为：2．