ΧβΡΩΡΎ»ί
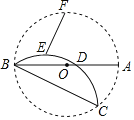
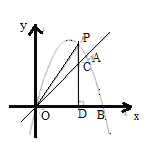
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABC «±Ώ≥ΛΈΣ2ΒΡΒ»±Ώ»ΐΫ«–ΈΘ§ΒψD”κΒψBΖ÷±πΈΜ”Ύ÷±œΏACΒΡΝΫ≤ύΘ§«“AD=AC, ΝΣΫαBDΓΔCDΘ§BDΫΜ÷±œΏAC”ΎΒψE.
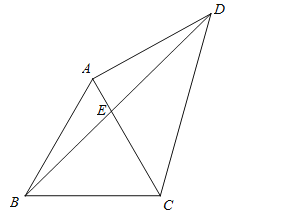

Θ®1Θ©Β±ΓœCAD=90Γψ ±Θ§«σœΏΕΈAEΒΡ≥Λ.
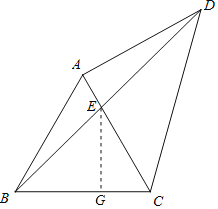
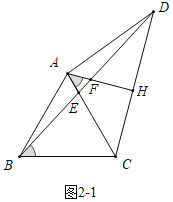
Θ®2Θ©ΙΐΒψAΉςAHΓΆCDΘ§¥ΙΉψΈΣΒψHΘ§÷±œΏAHΫΜBD”ΎΒψFΘ§
ΔΌΒ±ΓœCAD<120Γψ ±Θ§…η![]() Θ§
Θ§![]() Θ®Τδ÷–
Θ®Τδ÷–![]() ±μ ΨΓςBCEΒΡΟφΜΐΘ§
±μ ΨΓςBCEΒΡΟφΜΐΘ§![]() ±μ ΨΓςAEFΒΡΟφΜΐΘ©Θ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘΜ
±μ ΨΓςAEFΒΡΟφΜΐΘ©Θ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘΜ
ΔΎΒ±![]() ±Θ§«κ÷±Ϋ”–¥≥ωœΏΕΈAEΒΡ≥Λ.
±Θ§«κ÷±Ϋ”–¥≥ωœΏΕΈAEΒΡ≥Λ.
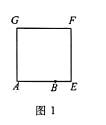
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©
Θ®2Θ©![]() (
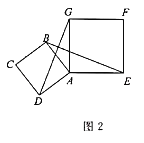
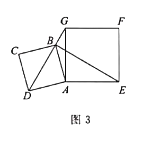
(![]() )ΘΜΘ®3Θ©
)ΘΜΘ®3Θ©![]() Μρ
Μρ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψ![]() Ής
Ής![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() Θ°
Θ°![]() Θ§‘ρ
Θ§‘ρ![]() Θ°ΗυΨί
Θ°ΗυΨί![]() ΙΙΫ®ΖΫ≥Χ«σ≥ω
ΙΙΫ®ΖΫ≥Χ«σ≥ω![]() Φ¥Ω…ΫβΨωΈ ΧβΘ°
Φ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©ΔΌ÷ΛΟς![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() Θ§”…¥ΥΙΙΫ®ΙΊœΒ ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ§”…¥ΥΙΙΫ®ΙΊœΒ ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΔΎΖ÷ΝΫ÷÷«ι–ΈΘΚΒ±![]() ±Θ§Β±
±Θ§Β±![]() ±Θ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
±Θ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΫβΘΚΘ®1Θ©![]() «Β»±Ώ»ΐΫ«–ΈΘ§
«Β»±Ώ»ΐΫ«–ΈΘ§
![]() Θ§
Θ§![]() Θ°
Θ°
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ°
Θ°
ΙΐΒψ![]() Ής
Ής![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() Θ°
Θ°
…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°
‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§
![]()
![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
ΫβΒΟ![]() Θ°
Θ°
Υυ“‘œΏΕΈ![]() ΒΡ≥Λ «
ΒΡ≥Λ «![]() Θ°
Θ°
Θ®2Θ©ΔΌ…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ°
Θ°
![]() Θ§
Θ§![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
”÷![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
”÷![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
”…Θ®1Θ©ΒΟ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§
![]()
![]() Θ°
Θ°
ΔΎΒ±![]() ±Θ§
±Θ§
![]() Θ§‘ρ”–
Θ§‘ρ”–![]() Θ§
Θ§
’ϊάμΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Μρ
Μρ![]() Θ®…αΤζΘ©Θ§
Θ®…αΤζΘ©Θ§
![]() Θ°
Θ°
Β±![]() ±Θ§Ά§Ζ®Ω…ΒΟ
±Θ§Ά§Ζ®Ω…ΒΟ![]()
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
’ϊάμΒΟ![]() Θ§
Θ§
ΫβΒΟ![]() Θ®…αΤζΘ©Μρ1Θ§
Θ®…αΤζΘ©Μρ1Θ§
![]() Θ°
Θ°
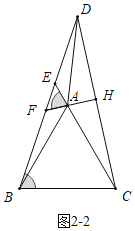
Ήέ…œΥυ ωΘΚΒ±ΓœCAD<120Γψ ±Θ§![]() ΘΜ Β±120Γψ<ΓœCAD<180Γψ ±Θ§
ΘΜ Β±120Γψ<ΓœCAD<180Γψ ±Θ§![]() .
.

 Κ°ΦΌ¥σ¥°ΝΣΜΤ…Ϋ ι…γœΒΝ–¥πΑΗ
Κ°ΦΌ¥σ¥°ΝΣΜΤ…Ϋ ι…γœΒΝ–¥πΑΗ Κ°ΦΌ¥¥–¬–ΆΉ‘÷ς―ßœΑΒΎ»ΐ―ßΤΎΚ°ΦΌœΈΫ”œΒΝ–¥πΑΗ
Κ°ΦΌ¥¥–¬–ΆΉ‘÷ς―ßœΑΒΎ»ΐ―ßΤΎΚ°ΦΌœΈΫ”œΒΝ–¥πΑΗ