题目内容
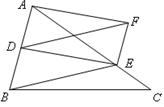
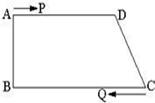
如图,已知长方形的每个角都是直角,将长方形ABCD沿EF折叠后点B恰好落在CD边上的点H处,且∠CHE=40 º.

(1)求∠HFA的度数;(2)求∠HEF的度数.

(1)求∠HFA的度数;(2)求∠HEF的度数.
(1)130°;(2)65°
试题分析:(1)根据平行线的性质可得∠CHF=∠HFA,根据折叠的性质可得∠EHF=∠B=90°,由∠CHE=40 º,可求得∠CHF的度数,即可求得结果;
(2)先根据三角形的内角和定理求得∠HEC的度数,再根据折叠的性质求解即可.
(1)∵DC∥AB
∴∠CHF=∠HFA
由折叠后可知,∠EHF=∠B=90°
∵∠CHE=40 º,
∴∠CHF=∠EHF+∠CHE ="90°+40" º=130°
∴∠HFA=∠CHF=130°;
(2)在⊿CHE中,
∵∠CHE+∠C+∠HEC=180°
∴∠HEC=180°-(∠CHE+∠C) =180°-(90°+40°) =50°
由折叠可知:∠HEF=∠BEF
∴∠HEF =
 (180°-∠HEC)=
(180°-∠HEC)= (180°-50 º)=65°.
(180°-50 º)=65°.点评:解题的关键是熟练掌握折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等,对应点的连线段被折痕垂直平分.

练习册系列答案
相关题目




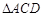 的面积为3,则图中阴影部分两个三角形的面积和为 .
的面积为3,则图中阴影部分两个三角形的面积和为 .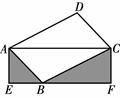
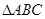 中,D是AB中点,E是AC上的点,且
中,D是AB中点,E是AC上的点,且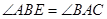 ,EF∥AB,DF∥BE,
,EF∥AB,DF∥BE,