��Ŀ����
����Ŀ��������һ������̽������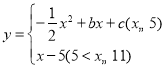 ��b��cΪ��������ͼ������ʣ�ԪԪ����ѧϰ�����ľ��飬�Ըú�����ͼ������ʽ���������̽����
��b��cΪ��������ͼ������ʣ�ԪԪ����ѧϰ�����ľ��飬�Ըú�����ͼ������ʽ���������̽����
������ԪԪ��̽�����̣����㲹������
x | ���� | ��1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ���� |
y | ���� | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | ���� |
��1�������ϱ���Ϣ������b��____��c��_____��m��______��
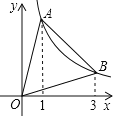
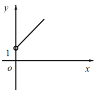
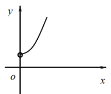
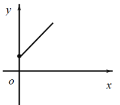
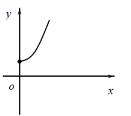
��2����ͼ��������ƽ��ֱ������ϵ�У�����Բ�ȫ��ı��и���ӦֵΪ����ĵ㣬�������ú�������һ����ͼ��
��3���۲캯��ͼ����д���ú�����һ�����ʣ�______��
��4��������⣺��ֱ��y��3n+2��nΪ��������ú���ͼ����3������ʱ����n�ķ�Χ��
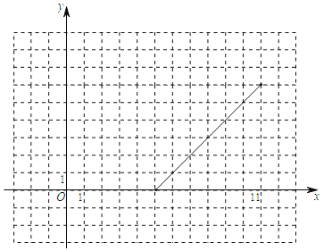
���𰸡���1��2��2.5��4.5����2������������3����x��2ʱ��y��x�����������4����![]() ��n��
��n��![]() ��
��
��������
��1�����ô���ϵ�����Լ����κ���ͼ���ϵ�����������ɵô𰸣�
��3��������㷨������ͼ�ɵô𰸣�
��4������ͼ��ı仯���ƣ��ɵô𰸣�
��5������ͼ�ɵô𰸣�
�⣺��1���ɱ������ݵã���x����1ʱ��y��0����x��5ʱ��y��0����x��0ʱ��y��2.5��
��b��![]() ��2��c��2.5
��2��c��2.5
��y��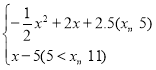
�൱x��2ʱ��y��4.5����m��4.5
�ʴ�Ϊ��2��2.5��4.5��
��2��ͼ�����£�
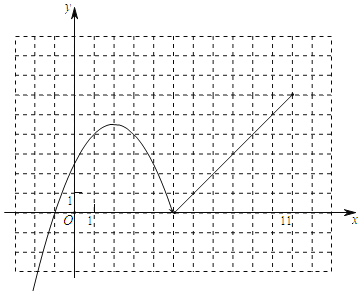
��3���۲�ͼ���֪����x��2ʱ��y��x�����������
�ʴ�Ϊ����x��2ʱ��y��x�����������
��4���ߵ�x��2ʱ��y��4.5��
����ͼ���ֱ֪��y��4.5��ú���ͼ����2�����㣬ֱ��y��0��ú���ͼ����2�����㣬
��ֱ��y��3n+2��nΪ��������ú���ͼ����3������ʱ��0��3n+2��4.5
�ੁ![]() ��n��
��n��![]() ��
��

 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д� �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�