题目内容
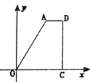
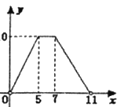
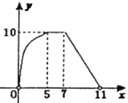
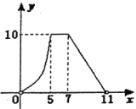
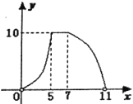
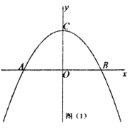
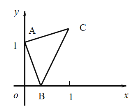
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.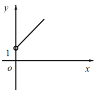 B.
B.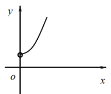
C.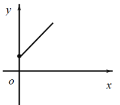 D.
D.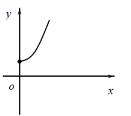
【答案】A
【解析】
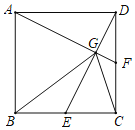
先做出合适的辅助线,再证明△ADC和△AOB的关系,即可建立y与x的函数关系,从而确定函数图像.
解:由题意可得:OB=x,OA=1,∠AOB=90°,∠BAC=90°,AB=AC,点C的纵坐标是y,
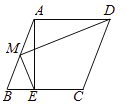
作AD∥x轴,作CD⊥AD于点D,如图所示:
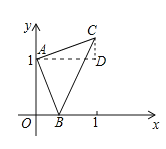
∴∠DAO+∠AOD=180°,
∴∠DAO=90°,
∴∠OAB+∠BAD=∠BAD+∠DAC=90°,
∴∠OAB=∠DAC,
在△OAB和△DAC中,
∠AOB=∠ADC,∠OAB=∠DAC,AB=AC
∴△OAB≌△DAC(AAS),
∴OB=CD,
∴CD=x,
∵点C到x轴的距离为y,点D到x轴的距离等于点A到x的距离1,
∴y=x+1(x>0).
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】有这样一个问题探究函数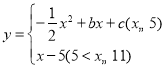 (b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:
(b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:
下面是元元的探究过程,请你补充完整
x | …… | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …… |
y | …… | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | …… |
(1)根据上表信息,其中b=____,c=_____,m=______.
(2)如图,在下面平面直角坐标系中,描出以补全后的表中各对应值为坐标的点,并画出该函数的另一部分图象;
(3)观察函数图象,请写出该函数的一条性质:______.
(4)解决问题:若直线y=3n+2(n为常数)与该函数图象有3个交点时,求n的范围.