题目内容
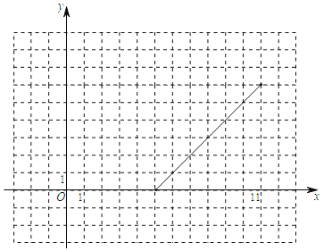
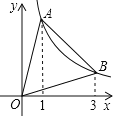
【题目】如图,AB是反比例函数y=![]() 在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,则S△AOB=_____.
在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,则S△AOB=_____.
【答案】4
【解析】
先根据反比例函数图象上点的坐标特征及A,B两点的横坐标,求出A(1,3),B(3,1).再过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,根据反比例函数系数k的几何意义得出S△AOC=S△BOD=![]() ×3=
×3=![]() .根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=
.根据S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,得出S△AOB=S梯形ABDC,利用梯形面积公式求出S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() (1+3)×2=4,从而得出S△AOB=4.
(1+3)×2=4,从而得出S△AOB=4.
解:∵A,B是反比例函数y=![]() 在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,
在第一象限内的图象上的两点,且A、B两点的横坐标分别是1和3,
∴当x=1时,y=3,即A(1,3),
当x=3时,y=1,即B(3,1).
如图,过A,B两点分别作AC⊥x轴于C,BD⊥x轴于D,则S△AOC=S△BOD=![]() ×3=
×3=![]() .
.
∵S四边形AODB=S△AOB+S△BOD=S△AOC+S梯形ABDC,
∴S△AOB=S梯形ABDC,
∵S梯形ABDC=![]() (BD+AC)CD=
(BD+AC)CD=![]() (1+3)×2=4,
(1+3)×2=4,
∴S△AOB=4.
故答案为4.

【题目】有这样一个问题探究函数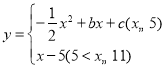 (b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:
(b、c为常数)的图象和性质.元元根据学习函数的经验,对该函数的图象和性质进行了以下探究:
下面是元元的探究过程,请你补充完整
x | …… | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …… |
y | …… | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | …… |
(1)根据上表信息,其中b=____,c=_____,m=______.
(2)如图,在下面平面直角坐标系中,描出以补全后的表中各对应值为坐标的点,并画出该函数的另一部分图象;
(3)观察函数图象,请写出该函数的一条性质:______.
(4)解决问题:若直线y=3n+2(n为常数)与该函数图象有3个交点时,求n的范围.