题目内容
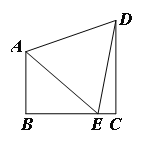
【题目】如图,四边形ABCD,∠B=∠C=90°,边BC上一点E,连结AE、DE得等边△ABC,若![]() =
=![]() ,则
,则![]() =_____
=_____
【答案】![]()
【解析】
延长CB至M,使∠AMB=60°,延长BC至N,使∠DNC=60°,由直角三角形的性质得出BM=![]() AM,CN=
AM,CN=![]() DN,证明△ABM∽△DCN,得出
DN,证明△ABM∽△DCN,得出![]() ,设AM=2a,则DN=3a,BM=
,设AM=2a,则DN=3a,BM=![]() AM=a,CN=
AM=a,CN=![]() DN=
DN=![]() ,证明△AME≌△END(AAS),得出AM=EN=2a,ME=ND=3a,求出BE=ME-BM=2a,CE=
,证明△AME≌△END(AAS),得出AM=EN=2a,ME=ND=3a,求出BE=ME-BM=2a,CE=![]() =
=![]() ,即可得出答案.
,即可得出答案.
解:延长CB至M,使∠AMB=60°,延长BC至N,使∠DNC=60°,如图所示:
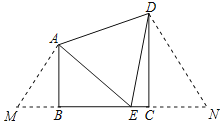
∵∠ABC=∠DCB=90°,
∴∠ABM=∠DCN=90°,
∴∠BAM=∠CDN=30°,
∴BM=![]() AM,CN=
AM,CN=![]() DN,△ABM∽△DCN,
DN,△ABM∽△DCN,
∴![]() ,
,
设AM=2a,则DN=3a,BM=![]() AM=a,CN=
AM=a,CN=![]() DN=
DN=![]() ,
,
∵△AED是等边三角形,
∴AE=DE,∠AED=60°,
∴∠AEM+∠NED=120°,
∵∠MAE+∠AEM=120°,
∴∠MAE=∠NED,
在△AME和△END中,
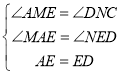 ,
,
∴△AME≌△END(AAS),
∴AM=EN=2a,ME=ND=3a,
∴BE=ME-BM=2a,CE=![]() =
=![]() ,
,
∴![]() ;
;
故答案为:![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目