Question

【题目】综合与实践

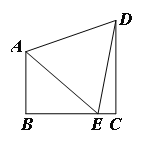
问题情境：如图1，在正方形中，点是对角线上的一点，点在的延长线上，且，交于点．问题解决：

（1）求证：；

（2）求的度数；

探索发现：

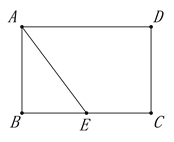
（3）如图2，若点在边上，且，求的度数．

Answer 1

【答案】（1）证明见解析；（2）90°；（3）90°

【解析】

（1）证明，利用全等三角形的性质等量代换即可得到结论；

（2）利用全等三角形的性质和等腰三角形的性质证得，又知，然后在△EDG和△CFG中利用三角形的内角和定理即可得出；

（3）过点作，，先证得四边形是正方形，然后证出，根据全等三角形的对应角相等，利用角的和差关系变形即可得出答案.

（1）证明：∵四边形是正方形，

∴，．

在和中，

∴．

∴．

∵，

∴．

（2）解：由（1）知，，

∴．

∵，

∴．

∴．

∵（对顶角相等），

∴．

即．

（3）解：过点作，，垂足分别为，．

∴．

同（1）可证，

∴，

∵四边形是正方形，

∴，，

∴，

又∵，

∴四边形是正方形，

∴，，

∵，

∴，

∴．

∴，

∴．