题目内容
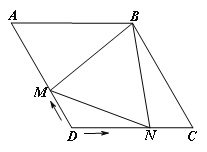
【题目】如图,菱形ABCD,∠A=60°,AB=6,点M从点D向点A以1个单位∕秒的速度运动,同时点N从点D向点C以2个单位∕秒的速度运动,连结BM、BN,当△BMN为等边三角形时,![]() =_____.
=_____.
【答案】![]()
【解析】
连接BD,证明△ABM≌△DBN,由此得到AM=DN,据此可求出运动时间为2秒,从而得到MD=2,DN=4.在△MDN中求出MN值,根据等边△面积公式即可求解.
解:连接BD,如图1所示:
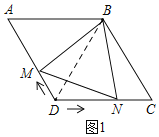
若△BMN是等边三角形,则BM=BN,∠MBN=60°.
∴∠DBN+∠MBD=60°.
∵四边形ABCD是菱形,∠A=60°,
∴AB=BD,∠ABD=60°.
∴∠ABM+∠MBD=60°,
∴∠ABM=∠DBN.
∴△ABM≌△DBN(SAS).
∴AM=DN.
设运动时间为t,则6-t=2t,解得t=2.
所以DM=2,DN=4.
如图2,过M点作MH⊥DN,交ND延长线于H点,
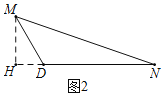
∵∠MDN=120°,
∴∠MDH=60°,
∴在Rt△MDH中,HD=![]() MD=1,MH=
MD=1,MH=![]() .
.
在Rt△MHN中,利用勾股定理可得MN=![]() .
.
∴等边三角形的边长为![]() .
.
∴等边三角形BMN的面积=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目