题目内容
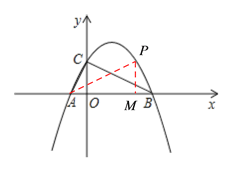
【题目】如图,二次函数y=-x2+ax+b的图象与x轴交于A(-![]() ,0),B(2,0)两点,且与y轴交于点C.
,0),B(2,0)两点,且与y轴交于点C.
(1)求该抛物线的解析式,并判断△ABC的形状;
(2)设P是x轴上方的抛物线上的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、A 、M为顶点的三角形与ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)见解析;(2)P(![]() ,1 ) (0,1).
,1 ) (0,1).
【解析】试题分析:
(1)由已知条件可设二次函数的解析式为: ![]() ,化简整理为一般形式即可;由所得解析式可得点C的坐标为(0,1),再由勾股定理求得AC2、BC2、AB2,最后由勾股定理的逆定理可得△ABC是直角三角形;
,化简整理为一般形式即可;由所得解析式可得点C的坐标为(0,1),再由勾股定理求得AC2、BC2、AB2,最后由勾股定理的逆定理可得△ABC是直角三角形;
(2)由(1)可知∠ACB=90°,由PM⊥x轴可得∠PMA=90°,即∠ACB=∠PMA=90°,
因此当:①![]() 或②
或②![]() 时,以点P、M、A为顶点的三角形与△ABC相似;设出点P的坐标,分以上两种情况讨论、计算即可.
时,以点P、M、A为顶点的三角形与△ABC相似;设出点P的坐标,分以上两种情况讨论、计算即可.
试题解析:
(1)二次函数![]() 的图象与
的图象与![]() 轴交于A
轴交于A![]() ,B
,B![]() 两点,
两点,
∴ 抛物线的解析式为![]() ,即:
,即: ![]() ;
;
∴点C的坐标为(0,1);
∴AC2=AO2+CO2=![]() ,
,
BC2= BO2+CO2=5,
AB2=![]() ;
;
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°;
(2)如图,∵PM⊥x轴,
∴∠PMA=90°,
∵∠ACB=90°,
∴∠ACB=∠PMA.
所以当: ![]() 或
或![]() 时,以点P、M、A为顶点的三角形与△ABC相似,
时,以点P、M、A为顶点的三角形与△ABC相似,
由点P在二次函数![]() 的图象上,可设其坐标为:
的图象上,可设其坐标为: ![]() ,
,
则由已知可得:PM=![]() ,AM=
,AM= ![]() ,由此可得:
,由此可得:
![]() 或
或![]() ,
,
解得: ![]() (不合题意,舍去)或
(不合题意,舍去)或![]() (不合题意,舍去),
(不合题意,舍去),
∴存在点P使以点P、M、A为顶点的三角形与△ABC相似,其坐标分别为: ![]() 和
和![]() .
.

练习册系列答案
相关题目