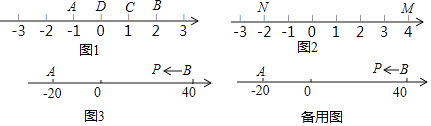��Ŀ����
����Ŀ����ͼ����A��ԭ����������������˶���ͬʱ����BҲ��ԭ����������������˶���2����������16����λ���ȣ���֪��B���ٶ��ǵ�A���ٶȵ�3�������ٶȵ�λ����λ����/�룩
![]()
��1�������A��B�˶����ٶȣ����������ϱ��A��B�����ԭ������˶�2��ʱ��λ�ã�
��2����A��B����ӣ�1���б����λ�ÿ�ʼ������ԭ�����ٶ�ͬʱ�����������˶�����t���
�ٵ�A�������ϵ�λ�ñ�ʾ����Ϊ�� ������B�������ϵ�λ�ñ�ʾ����Ϊ�� �������ú�t�Ĵ���ʽ��ʾ��
�ڵ�tΪ����ʱ����A��B֮�����4����λ���ȣ�
���𰸡���1��������; ��2���٩�4��2t�� 12��6t����3��5�룮
��������
(1)���A���ٶ�Ϊÿ��t����λ����,���B���ٶ�Ϊÿ��3t����λ����,�������:��A�˶��ľ���+��B�˶��ľ���=16,���ݵ�����ϵ,�г�����,�ٽⷽ�̼���.
(2)����ԭ���Ļ�����,��ȥ�����˶��ľ��뼴�ɵ�.
�ڸ��������ľ��빫ʽ�г�����t�ķ���,��֮����.
�⣺��1�����A���ٶ�Ϊÿ��t����λ���ȣ����B���ٶ�Ϊÿ��3t����λ���ȣ�
��������2t+2��3t=16�����t=2��
���A���ٶ�Ϊÿ��2����λ���ȣ���B���ٶ�Ϊÿ��6����λ���ȣ�
��ͼ
![]()
��2���ٵ�A�����˶�t�������ʾ����Ϊ��4��2t����B�����˶�t�������ʾ����Ϊ12��6t��
�ڸ���������6t��2t=16��4����ã�t=3��
��6t��2t=16+4�����t=5��
���˶�3��5��ʱ����A��B֮�����4����λ���ȣ�
�ʴ�Ϊ����4��2t��12��6t��