题目内容
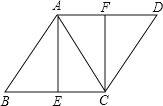
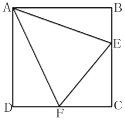
【题目】如图，E与F分别在正方形ABCD边BC与CD上，∠EAF=45°.
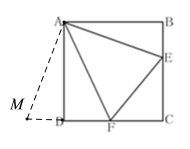
（1）以A为旋转中心，将△ABE按顺时针方向旋转90°，画出旋转后得到的图形.
（2）已知BE=2cm，DF=3cm，求EF的长.
【答案】（1）见解析；（2）5cm.
【解析】（1）根据旋转角度、旋转方向、旋转点找出各点的对应点，顺次连接即可得出；
（2）首先证明△ABE≌△ADM，进而得到∠MAF=45°；证明△EAF≌△MAF，得到EF=FG问题即可解决．
（1）如图所示；
（2）由（1）知：△ADM≌△ABE，M、D、F共线，
∴AD=AB，AM=AE，∠MAD=∠BAE，MD=BE=2，
∵四边形ABCD为正方形，∠EAF=45°，∴∠BAE+∠DAF=45°，
∴∠MAD+∠DAF=45°，
∴△AMF≌△AEF(SAS)，
∴EF=MF，
∵MF=MD+DF，
∴EF=MF=MD+DF=2+3=5cm.
练习册系列答案
相关题目
