��Ŀ����
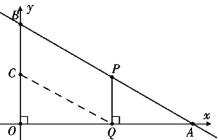
����Ŀ����֪��ͼ��ֱ��AB����ʽΪ![]() ����ͼ����������x,y��ֱ��ཻ��A��B���㣬��P���߶�AB����A��B����ÿ��2����λ�˶�����C���߶�OB����O��B����ÿ��1����λ�˶�������һ���ȵ����յ���ֹͣ�˶���������P��x�ᴹֱ��ֱ�߽�ֱ��AO�ڵ�Q. ���˶���ʱ��Ϊt�루t��0��.
����ͼ����������x,y��ֱ��ཻ��A��B���㣬��P���߶�AB����A��B����ÿ��2����λ�˶�����C���߶�OB����O��B����ÿ��1����λ�˶�������һ���ȵ����յ���ֹͣ�˶���������P��x�ᴹֱ��ֱ�߽�ֱ��AO�ڵ�Q. ���˶���ʱ��Ϊt�루t��0��.
��1��ֱ��д����A��B���������A( )��B( ).
��BAO=______________�ȣ�
��2���ú�t�Ĵ���ʽ�ֱ��ʾ��CB�� ��PQ�� ��
��3���Ƿ����t��ֵ��ʹ�ı���PBCQΪƽ���ı��Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��4����3�֣��Ƿ����t��ֵ��ʹ�ı���PBCQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��̽����θı��C���ٶȣ������˶�����ʹ�ı���PBCQ��ijһʱ��Ϊ���Σ����C���ٶȺ�ʱ
��t.
���𰸡���1��![]() ����BAO=30�㣻��2��
����BAO=30�㣻��2��![]() ����3��������;(4) ����C���ٶȱ�Ϊÿ��
����3��������;(4) ����C���ٶȱ�Ϊÿ��![]() ����λʱ��
����λʱ��![]() ʱ�ı���PBCQ������.
ʱ�ı���PBCQ������.
��������(1)��x=0,y=0�ɷֱ����A,B�����ꣻ��2��������IJ�����߶γ��ȣ���3����PQ=BCʱ �� ��![]() ����ƽ���ı��Σ���4��
����ƽ���ı��Σ���4��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ���Բ����������Σ����ı���PBCQ����������
���Բ����������Σ����ı���PBCQ����������![]() ��PQ=BC��
��PQ=BC��
��PQ=PBʱ����.
�⣺��1��ֱ��д����A��B���������![]() ����BAO=30��
����BAO=30��
��2���ú�t�Ĵ���ʽ�ֱ��ʾ��![]() ��
��
��3����![]()
�൱PQ=BCʱ �� ��![]() ��
��![]() ʱ���ı���PBCQ��ƽ���ı���.
ʱ���ı���PBCQ��ƽ���ı���.
��4����![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]()
���ı���PBCQ���ܹ������Ρ�
���ı���PBCQ����������![]() ��PQ=BC��
��PQ=BC��
��PQ=PBʱ����.
����![]() ʱ
ʱ
BC=BP=PQ=![]() OC=OB-BC=
OC=OB-BC=![]()

�൱��C���ٶȱ�Ϊÿ��![]() ����λʱ��
����λʱ��![]() ʱ�ı���PBCQ������.
ʱ�ı���PBCQ������.

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�