Question

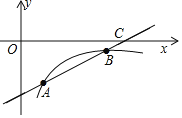
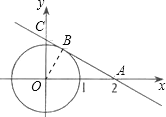
【题目】如图⊙O的半径为1，过点A（2，0）的直线切⊙O于点B，交y轴于点C．

（1）求线段AB的长；

（2）求以直线AC为图象的一次函数的解析式．

Answer 1

【答案】(1);(2) y=-x+.

【解析】

（1）由于直线AC是⊙O的切线，B为切点，所以需连接OB，利用切线的性质得OB⊥AB，在Rt△AOB中，利用勾股定理，求出AB的长．

（2）要求直线AC的解析式，需知A、C两点的坐标，易证△ABO∽△AOC，利用相似三角形的性质求得C点坐标，设解析式为y=kx+b，将A、C两点代入求出k、b的值即可．

解：（1）连接OB，

∵AC切⊙O于点B，

∴OB⊥AC，
∴AB==；

（2）∵∠A=∠A，∠ABO=∠AOC，
∴△ABO∽△AOC，
∴=，即：=，
解得：OC=，
∴点C坐标为（0，），
设一次函数的解析式为：y=kx+，将点A（2，0）代入，解得：k=-，
∴以直线AC为图象的一次函数的解析式为：y=-x+．