题目内容
【题目】如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.
(1)求证:PABD=PBAE;
(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
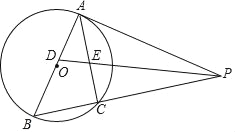
【答案】(1)证明见解析;(2)存在,![]()
【解析】(1)易证∠APE=∠BPD,∠EAP=∠B,从而可知△PAE∽△PBD,利用相似三角形的性质即可求出答案.
(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,易求得AE=2,BD=3,由(1)可知:![]() ,从而可知cos∠BDF=cos∠BAC=cos∠APC=
,从而可知cos∠BDF=cos∠BAC=cos∠APC=![]() ,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
,从而可求出AD和DG的长度,进而证明四边形ADFE是菱形,此时F点即为M点,利用平行四边形的面积即可求出菱形ADFE的面积.
(1)∵PD平分∠APB,
∴∠APE=∠BPD,
∵AP与⊙O相切,
∴∠BAP=∠BAC+∠EAP=90°,
∵AB是⊙O的直径,
∴∠ACB=∠BAC+∠B=90°,
∴∠EAP=∠B,
∴△PAE∽△PBD,
∴![]() ,
,
∴PABD=PBAE;
(2)如图,过点D作DF⊥PB于点F,作DG⊥AC于点G,
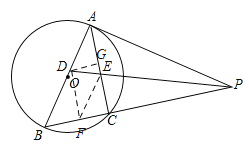
∵PD平分∠APB,AD⊥AP,DF⊥PB,
∴AD=DF,
∵∠EAP=∠B,
∴∠APC=∠BAC,
易证:DF∥AC,
∴∠BDF=∠BAC,
由于AE,BD(AE<BD)的长是x2﹣5x+6=0的两个实数根,
解得:AE=2,BD=3,
∴由(1)可知:![]() ,
,
∴cos∠APC=![]() ,
,
∴cos∠BDF=cos∠APC=![]() ,
,
∴![]() ,
,
∴DF=2,
∴DF=AE,
∴四边形ADFE是平行四边形,
∵AD=DF,
∴四边形ADFE是菱形,此时点F即为M点,
∵cos∠BAC=cos∠APC=![]() ,
,
∴sin∠BAC=![]() ,
,
∴![]() ,
,
∴DG=![]() ,
,
∴菱形ADME的面积为:DGAE=2×![]() =
=![]() .
.