题目内容
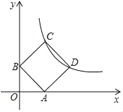
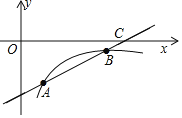
【题目】如图，一次函数y=kx+b的图象交反比例函数y=
（x＞0）的图象于A（4，-8）、B（m，-2）两点，交x轴于点C．
（1）求反比例函数与一次函数的关系式；
（2）根据图象回答：当x为何值时，一次函数的值大于反比例函数的值？
（3）以O、A、B、P为顶点作平行四边形，请直接写出点P的坐标．
【答案】（1）反比例函数关系式为
，一次函数关系式为
．（2）0＜x＜4或x＞16；（3）P的坐标为（12，6）或（-12，-6）或（20，-10）．
【解析】
（1）将点A（4，-8），B（m，-2）代入反比例函数y=
（x＞0）中，可求k、a；再将点A（4，-8），B（m，-2）代入y=kx+b中，列方程组求k、b即可；
（2）根据两函数图象的交点，图象的位置可确定一次函数的值大于反比例函数的值时x的范围；
（3）根据平行四边形的性质，即可直接写出．
解：（1）∵反比例函数y=（x＞0）的图象于A（4，-8），
∴k=4×（-8）=-32．
∵双曲线y=过点B（m，-2），
∴m=16．
由直线y=kx+b过点A，B得：
，
解得，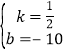
，
∴反比例函数关系式为，一次函数关系式为．
（2）观察图象可知，当0＜x＜4或x＞16时，一次函数的值大于反比例函数的值．
（3）∵O（0，0），A（4，-8）、B（16，-2），
分三种情况：①若OB∥AP，OA∥BP，
∵O（0，0），A（4，-8），
∴由平移规律，点B（16，-2）向右平移4个单位，向下平移8个单位得到P点坐标为（20，-10）；
②若OP∥AB，OA∥BP，
∵A（4，-8），B（16，-2），
∴由平移规律，点O（0，0）向右平移12个单位，向上平移6个单位得到P点坐标为（12，6）；
③若OB∥AP，OP∥AB，
∵B（16，-2），A（4，-8），
∴由平移规律，点O（0，0）向左平移12个单位，向下平移6个单位得到P点坐标为（-12，-6）；
∴以O，A，B，P为顶点作平行四边形，第四个顶点P的坐标为（12，6）或（-12，-6）或（20，-10）．
