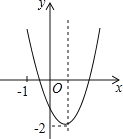题目内容
【题目】已知![]() ,以
,以![]() 为边在
为边在![]() 外作等腰
外作等腰![]() ,其中
,其中![]() .
.

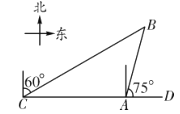
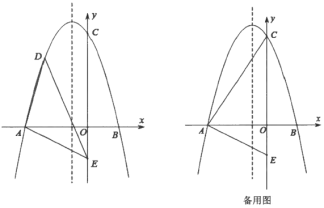
(1)如图1,若![]() 为边在
为边在![]() 外作
外作![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
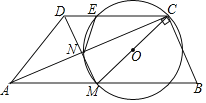
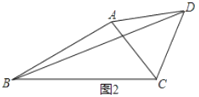
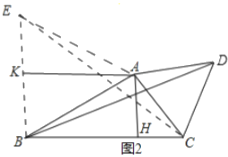
(2)如图2,![]() ,
,![]() ,
,![]() ,
,![]() .
.
①若![]() ,
,![]() ,
,![]() 的长为 ;
的长为 ;
②若改变![]() 、
、![]() 的大小,但
的大小,但![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)证明![]() ,再根据三角形外角的性质即可得到答案;
,再根据三角形外角的性质即可得到答案;
(2)①以![]() 为边在
为边在![]() 外作正三角形
外作正三角形![]() ,连接
,连接![]() ,根据(1)求出
,根据(1)求出![]() ,根据勾股定理求出BE即可得到AB的长;
,根据勾股定理求出BE即可得到AB的长;
②作![]() 交
交![]() 于
于![]() ,过点
,过点![]() 作BE∥AH,并在
作BE∥AH,并在![]() 上取
上取![]() ,连接
,连接![]() ,
,![]() .并取
.并取![]() 的中点
的中点![]() ,连接
,连接![]() ,先证明四边形
,先证明四边形![]() 为平行四边形,根据
为平行四边形,根据![]() ,得到四边形
,得到四边形![]() 为矩形得到
为矩形得到![]() ,再证明
,再证明![]() 求出EC=ED=8,根据勾股定理求出AH即可求出面积.
求出EC=ED=8,根据勾股定理求出AH即可求出面积.
(1)如图1,
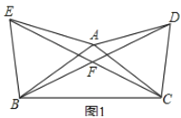
∵AE=AB,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
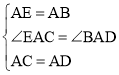 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)①如图2,以![]() 为边在
为边在![]() 外作正三角形
外作正三角形![]() ,连接
,连接![]() .
.
由(1)可知![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图2,作![]() 交
交![]() 于
于![]() ,过点
,过点![]() 作BE∥AH,并在
作BE∥AH,并在![]() 上取
上取![]() ,连接
,连接![]() ,
,![]() .并取
.并取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() 于
于![]() ,
,
∴![]() .
.
∵BE∥AH,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() .
.
∵BK∥AH,
∴四边形![]() 为平行四边形.
为平行四边形.
又∵![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() .
.
∴![]() 是
是![]() 的垂直平分线.
的垂直平分线.
∴![]() .
.
∵![]() ,AC=AD,
,AC=AD,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 与
与![]() 中,
中,
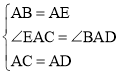 ,
,
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
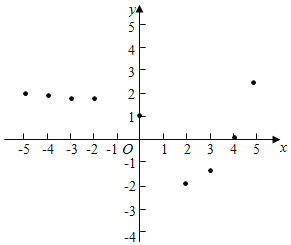
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .