Question

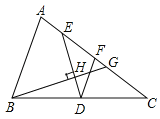
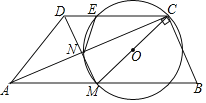
【题目】如图，在Rt△ABC中，M是斜边AB的中点，以CM为直径作圆O交AC于点N，延长MN至D，使ND＝MN，连接AD、CD，CD交圆O于点E．

(1)判断四边形AMCD的形状，并说明理由；

(2)求证：ND＝NE；

(3)若DE＝2，EC＝3，求BC的长．

Answer 1

【答案】(1)四边形AMCD是菱形，理由见解析；(2)证明见解析；(3)BC＝2．

【解析】

(1)证明四边形AMCD的对角线互相平分，且∠CNM＝90°，可得四边形AMCD为菱形；

(2)可证得∠CMN＝∠DEN，由CD＝CM可证出∠CDM＝∠CMN，则∠DEN＝∠CDM，结论得证；

(3)证出△MDC∽△EDN，由比例线段可求出ND长，再求MN的长，则BC可求出．

(1)四边形AMCD是菱形，理由如下：

∵M是Rt△ABC中AB的中点，

∴CM＝AM，

∵CM为⊙O的直径，

∴∠CNM＝90°，

∴MD⊥AC，

∴AN＝CN，

∵ND＝MN，

∴四边形AMCD是菱形；

(2)∵四边形CENM为⊙O的内接四边形，

∴∠CEN+∠CMN＝180°，

∵∠CEN+∠DEN＝180°，

∴∠CMN＝∠DEN，

∵四边形AMCD是菱形，

∴CD＝CM，

∴∠CDM＝∠CMN，

∴∠DEN＝∠CDM，

∴ND＝NE；

(3)∵∠CMN＝∠DEN，∠MDC＝∠EDN，

∴△MDC∽△EDN，

∴，

设DN＝x，则MD＝2x，由此得，

解得：x＝或x＝﹣(不合题意，舍去)，

∴，

∵MN为△ABC的中位线，

∴BC＝2MN，

∴BC＝2．