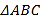题目内容
【题目】如图示,在平面直角坐标系中,二次函数![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
(1)求二次函数的表达式;
(2)点![]() 是第二象限内的点抛物线上一动点
是第二象限内的点抛物线上一动点
①求![]() 面积最大值并写出此时点
面积最大值并写出此时点![]() 的坐标;
的坐标;
②若![]() ,求此时点
,求此时点![]() 坐标;
坐标;
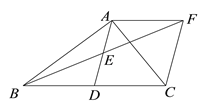
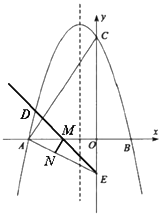
(3)连接![]() ,点
,点![]() 是线段
是线段![]() 上的动点.连接
上的动点.连接![]() ,把线段
,把线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 是点
是点![]() 的对应点.当动点
的对应点.当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,则动点
,则动点![]() 所经过的路径长等于______(直接写出答案)
所经过的路径长等于______(直接写出答案)
【答案】(1)![]() ;(2)①
;(2)①![]() ,点
,点![]() 坐标为
坐标为![]() ;②
;②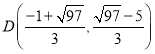 ;(3)
;(3)![]()
【解析】
(1)根据点坐标代入解析式即可得解;
(2)①由A、E两点坐标得出直线AE解析式,设点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() 坐标为
坐标为![]() ,然后构建
,然后构建![]() 面积与t的二次函数,即可得出
面积与t的二次函数,即可得出![]() 面积最大值和点D的坐标;
面积最大值和点D的坐标;
②过点![]() 作
作![]() ,在
,在![]() 中,由
中,由![]() ,
,![]() ,
,![]() 得出点M的坐标,进而得出直线ME的解析式,联立直线ME和二次函数,即可得出此时点D的坐标;
得出点M的坐标,进而得出直线ME的解析式,联立直线ME和二次函数,即可得出此时点D的坐标;
(3)根据题意,当点P在点C时,Q点坐标为(-6,6),当点P移动到点A时,Q′点坐标为(-4,-4),动点![]() 所经过的路径是直线QQ′,求出两点之间的距离即可得解.
所经过的路径是直线QQ′,求出两点之间的距离即可得解.
(1)依题意得:![]() ,解得
,解得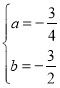
∴![]()
(2)①∵![]() ,
,![]()
∴设直线AE为![]()
将A、E代入,得![]()
∴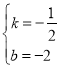
∴直线![]()
设点![]() 坐标为
坐标为![]() ,其中
,其中![]()
过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() 坐标为
坐标为![]()
∴![]()
∴![]()
即:![]()
由函数知识可知,当![]() 时,
时,![]() ,点
,点![]() 坐标为
坐标为![]()
②设![]() 与
与![]() 相交于点
相交于点![]()
过点![]() 作
作![]() ,垂足为
,垂足为![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴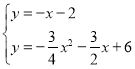
∴![]()
∴![]() (舍去),
(舍去),![]()
当![]() 时,
时,![]()
∴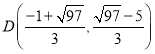
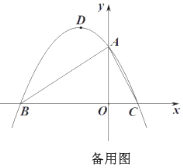
(3)当点P在点C时,Q点坐标为(-6,6),当点P移动到点A时,Q′点坐标为(-4,-4),如图所示:
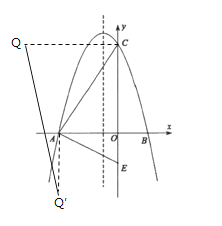
∴动点![]() 所经过的路径是直线QQ′,
所经过的路径是直线QQ′,
∴![]()
故答案为![]() .
.

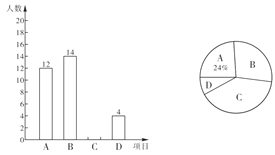
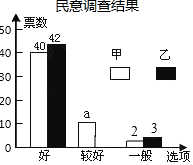
【题目】我校2019年度“一中好声音“校园歌手比赛已正式拉开序幕,其中甲,乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
A | B | C | D | E | F | |
甲 | 88 | m | 90 | 93 | 95 | 96 |
乙 | 89 | 92 | 90 | 97 | 94 | 93 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)六位评委对甲同学所打分数的平均分为92分,则m= ;
(3)学校规定评分标准:去掉评委评分中最高和最低分,再算平均分,并将平均分与民意测评分按3:2计算最后得分,求甲、乙两位同学的得分,(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
(4)现准备从甲、乙两位同学中选一位优秀同学代表重庆一中参加市歌手大赛,请问选哪位同学?并说明理由.
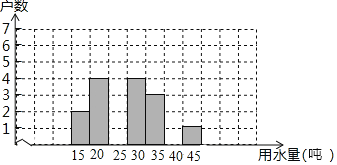
【题目】下表是2018年三月份某居民小区随机抽取20户居民的用水情况::
月用水量/吨 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
户数 | 2 | 4 | m | 4 | 3 | 0 | 1 |
(1)求出m= ,补充画出这20户家庭三月份用电量的条形统计图;
(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
统计量名称 | 众数 | 中位数 | 平均数 |
数据 |
|
|
|
(3)为了倡导“节约用水绿色环保”的意识,江赣市自来水公司实行“梯级用水、分类计费”,价格表如下:
月用水梯级标准 | Ⅰ级(30吨以内) | Ⅱ级(超过30吨的部分) |
单价(元/吨) | 2.4 | 4 |
如果该小区有500户家庭,根据以上数据,请估算该小区三月份有多少户家庭在Ⅰ级标准?
(4)按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?