Question

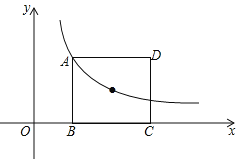
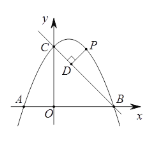
【题目】如图，直线y =－x+4与x轴，y轴分别交于点B，C，点A在x轴负半轴上，且OA=OB, 抛物线y =ax2+bx+4经过A，B，C三点．

（1）求抛物线的解析式；

（2）点P是第一象限内抛物线上的动点，设点P的横坐标为m，过点P作PD⊥BC，垂足为D，用含m的代数式表示线段PD的长，并求出线段PD的最大值；

（3）设点E为抛物线对称轴与直线BC的交点，若A，B，E三点到同一直线的距离分别是d1，d2，d3，问是否存在直线l，使得d1= d2=d3? 若存在，请直接写出d3的值，若不存在，请说明理由．

Answer 1

【答案】（1）y=－x2+ x+4；（2）当m=2时，PE最大，最大值为；（3）存在，满足题意的d3的值为2或6或．

【解析】

（1）由直线y=-x+4得出B（4，0），C（0，4），即可得出A（-2，0），将A与B坐标代入抛物线解析式求出a与b的值，即可确定出抛物线解析式；

（2）已知P点横坐标，根据直线AB、抛物线的解析式，求出C、P的坐标，由此得到线段PC的长；在Rt△OBC中，∠OCB=45°，根据平行线的性质得出∠PFD=45°，解直角三角形即可求出PD的表达式，利用二次函数的性质求出PD的最大值即可．

（3）见解析.

解:（1）由y=－x+4得 当x=0时，y=4； 当y=0时，x=4．

∴ B(4，0) ， C(0，4)， ∴ OB=4．

∴ OA=OB=2， ∴ 点 A(－2，0)．

把A(－2，0)，B(4，0)分别代入抛物线y=ax2+bx+4中，得

解得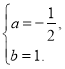

∴ 抛物线的解析式为 y=－x2+ x+4．

（2）∵ 点P的横坐标为m，则P(m，－m2+ m+4)．

过点P作PF∥y轴交BC于点F，则F(m，－m+4) ．

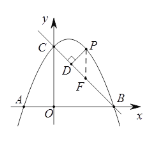
∴ PF=－m2+ m+4－(－m+4)=－m2+2m．

在Rt△OBC中，OB=4，OC=4．

又 PF∥y轴， ∴ ∠PFD=∠OCB=45°．

∴ PD=PF·sin∠PFD= PF·sin∠OCB =(－m2+2m)=－img src="http://thumb.zyjl.cn/questionBank/Upload/2020/10/22/06/64e53364/SYS202010220603483477190214_DA/SYS202010220603483477190214_DA.008.png" width="28" height="45" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />(m－2)2+．

∵ 0＜m＜4，－＜0，∴ 当m=2时，PE最大，最大值为．

（3）存在，∵y=－x2+ x+4=－（x-1）+，

∴C点坐标为（1,3），

如图，d1= d2=d3 ，

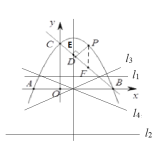
满足题意的d3的值为2或6或．