题目内容
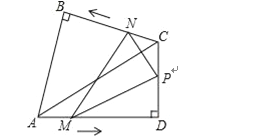
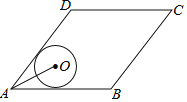
【题目】如图,菱形ABCD的边AB=5,面积为20,∠BAD<90°,⊙O与边AB、AD都相切,AO=2,则⊙O的半径长等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AC、BD、OE,根据菱形的性质、勾股定理分别求出AM、BM,根据切线的性质得到∠OEA=90°,证明△AOE∽△ABM,根据相似三角形的性质列出比例式,计算即可.
连接AC、BD、OE,
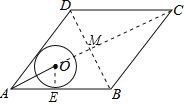
∵四边形ABCD是菱形,
∴AC⊥BD,AM=CM,BM=DM,
∵⊙O与边AB、AD都相切,
∴点O在AC上,
设AM=x,BM=y,
∵∠BAD<90°,
∴x>y,
由勾股定理得,x2+y2=25,
∵菱形ABCD的面积为20,
∴![]()
![]() xy=5,
xy=5,
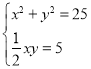
解得,x=2![]() ,y=
,y=![]() ,
,
∵⊙O与边AB相切,
∴∠OEA=90°,
∵∠OEA=∠BMA,∠OAE=∠BAM,
∴△AOE∽△ABM,
∴![]() ,即
,即![]()
解得,OE=![]() ,
,
故选:D.

练习册系列答案
相关题目
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
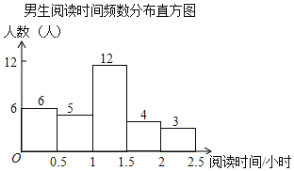
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?