题目内容
【题目】数学课上,潘老师给出如下定义:如果一个三角形有一边上的高线等于这条边的一半,那么称这个三角形为“垂美三角形”,这条边称为这个三角形的“垂美边”.
概念理解:
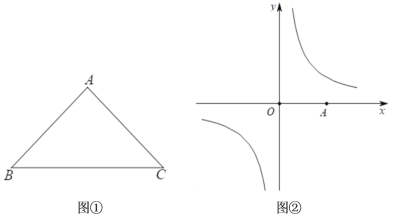
(1)如图①,已知∠A=90°,AB=AC,请证明等腰Rt△ABC一定是“垂美三角形”.
探索运用:
(2)已知等腰△ABC是“垂美三角形”,请求出顶角的度数.
能力提升:
(3)如图②,在直角坐标系中,点A为x轴正半轴上动点,在反比例函数![]() 的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
【答案】(1)证明见解析;(2)顶角为30°,90°或150°;(3)存在点B1(![]() ,1)、B2(-
,1)、B2(-![]() ,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边
,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边
【解析】
过点A作AH⊥BC于H,根据等腰三角形的三线合一即可求证;
分三种情况求∠BAC的度数:①若AB=AC,BC是“垂美边”; ②若BA=BC,BC是“垂美边”; ③若CA=CB,BC是“垂美边”
(3) 当△OAB是“垂美三角形”,且OA,OB均为“垂美边”,设△ABC的边OA、OB上的高分别记为ha、hb,则由“垂美三角形”的定义可知,ha=![]() OA, hb=
OA, hb=![]() OB.根据面积相等,得出OA=OB, ∠AOB的度数为30°或150°. 设B(m,
OB.根据面积相等,得出OA=OB, ∠AOB的度数为30°或150°. 设B(m,![]() )即可得出B点坐标
)即可得出B点坐标
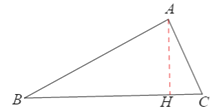
(1)证明:如图,过点A作AH⊥BC于H.

∵AB=AC,
∴H是BC中点,
∵∠BAC=90°,
∴AH=![]() BC,
BC,
∴等腰Rt△ABC是“垂美三角形”.
(2)①如图,若AB=AC,BC是“垂美边”,过点A做AH⊥BC于H.

则AH=BH=CH,且AH⊥BC,
∴∠B=∠C=45°,
∴∠BAC=90°;
②如图,若BA=BC,BC是“垂美边”,过点A做AH⊥BC于H,
则BC=2AH=AB,且AH⊥BC,
∴∠B=30°;
③如图,若CA=CB,BC是“垂美边”,过点A做AH⊥BC交BC的延长线于H,
则BC=2AH=AC,且AH⊥BC,

∴∠ACD=30°,从而∠ACB=150°.
综上所述,顶角为30°,90°或150°.
(3)当△OAB是“垂美三角形”,且OA,OB均为“垂美边”,设△ABC的边OA、OB上的高分别记为ha、hb,则由“垂美三角形”的定义可知,ha=![]() OA, hb=
OA, hb=![]() OB.
OB.
而S△ABC=![]() OA
OA![]() ha=
ha=![]() OA
OA![]() hb,
hb,
∴OA=OB.
由(2)可知,∠AOB的度数为30°或150°.
设B(m,![]() )则由“垂美三角形”的定义有:
)则由“垂美三角形”的定义有:![]() =
=![]() OA,从而OA2=
OA,从而OA2=![]() .
.
又OB2=m2+![]() ,则有OA=OB可得:
,则有OA=OB可得: ![]() ,解得m=
,解得m=![]() .
.
故存在点B1(![]() ,1)、B2(-
,1)、B2(-![]() ,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边”.
,-1),使△OAB是“垂美三角形”,且OA,OB均为“垂美边”.