题目内容
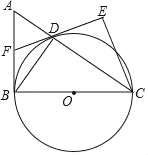
【题目】如图，已知直角△ABC中，∠ABC=90°，BC为圆O的直径，D为圆O与斜边AC的交点，DE为圆O的切线，DE交AB于F，且CE⊥DE．
（1）求证：CA平分∠ECB；
（2）若DE=3，CE=4，求AB的长；
（3）记△BCD的面积为S1，△CDE的面积为S2，若S1：S2=3：2．求sin∠AFD的值．
【答案】（1）详见解析；（2）
；（3）
.
【解析】
（1），连接OD，由DE是⊙O的切线可知OD⊥DE，由CE⊥DE，可知OD∥CE，进而可知∠ECD=∠CDO，因为∠CDO=∠DCO，所以∠ECD=∠DCO，即可证明.（2）连接BD，根据勾股定理可求出CD=5，所以tan∠ECD=
=
，在根据各直角三角形中各边的函数关系即可求出AB的长.（3）过点D作DG⊥BC于G，由CA∠BCE，可知DG=DE，进而△CDG≌△CDE根据S1：S2=3：2得
，得
，所以BC=3BG，OD=OC=
BC=
BG，根据勾股定理可求出DG得长，进而可求出sin∠DOG的值，根据四边形内角和可知∠AFD=∠DOG，即可求出sin∠AFD的值．
（1）如图，连接OD，
∵DE是⊙O的切线，
∴OD⊥DE，
∵CE⊥DE，
∴OD∥CE，
∴∠ECD=∠CDO，
∵∠CDO=∠DCO，
∴∠ECD=∠DCO，
∴CA平分∠ECB；
（2）如图，连接BD，∵BD为直径，
∴∠BDC=90°，
在Rt△CED中，DE=3，CE=4，根据勾股定理得，DC=5，
∴tan∠ECD==，
∴BD=DCtan∠DCB=
，
∵∠BCD+∠CBD=90°，∠ABD+∠CBD=90°，
∴∠BCD=∠ABD，
在Rt△CDE中，cos∠DCE=
=
，
∴cos∠BCD=，
∴cos∠ABD=，
在Rt△ABD中，cos∠ABD=
=，
∴AB=
×=；
（3）如图，
过点D作DG⊥BC于G，
∵CA平分∠BCE，
∴DG=DE，
易知，△CDG≌△CDE，
∴S2=S△CDG=S△CDE，
∵S1：S2=3：2，
∴
，
∴，
∴，
设BG=x，则CG=2x，
∴BC=BG+CG=3x，
∴OD=OC=BC=x，
∴OG=CG﹣OC=2x﹣x=x，
在Rt△ODG中，根据勾股定理得，DG=
x，sin∠DOG=
=
= ，
在四边形OBFD中，根据四边形内角和得，∠BFD+∠DOG=180°，
∵∠AFD+∠BFD=180°，
∴∠AFD=∠DOG，
∴sin∠AFD= ．
