题目内容
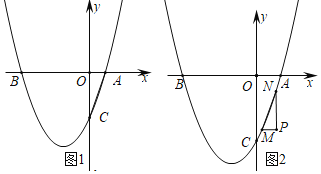
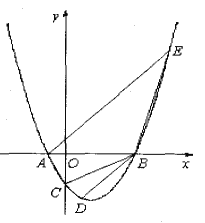
【题目】设抛物线![]() 与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线![]() 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
【答案】(1)m=4,y=![]() x2-
x2-![]() x-2;(2) (
x-2;(2) (![]() ,0)或 (-
,0)或 (-![]() ,0)
,0)
【解析】
(1)根据抛物线的解析式可知OC=2,由于∠ACB=90°,可根据△AOC∽△COB求出OB的长,即可得出B点的坐标,也就得出了m的值.然后根据A,B,C三点的坐标,用待定系数法可求出抛物线的解析式;
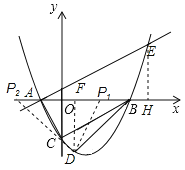
(2)先求出点D的坐标,然后分情况进行讨论,如果过E作x轴的垂线,不难得出∠DBx=135°,而∠ABE是个钝角但小于135°,因此P点只能在B点左侧.可分两种情况进行讨论:①∠DPB=∠ABE,即△DBP∽△EAB,可得出BP:AP=BD:AE,可据此来求出P点的坐标.②∠PDB=∠ABE,即△DBP∽△BAE,方法同①,只不过对应的成比例线段不一样.综上所述可求出符合条件的P点的值.
解:(1)令x=0,得y=-2,
∴C(0,-2),
∵∠ACB=90°,CO⊥AB,
∴△AOC∽△COB,
∴OAOB=OC2,
∴OB=![]() =
=![]() =4,
=4,
∴m=4,
∴B(4,0),
将A(-1,0),B(4,0)代入y=ax2+bx-2得![]() ,
,
解得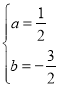 ,
,
∴抛物线的解析式为y=![]() x2-
x2-![]() x-2;
x-2;
(2)当x=1时,y=![]() -
-![]() - 2=-3,
- 2=-3,
∴D(1,-3 ).
解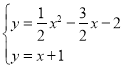 得,
得,![]() 或
或![]() ,
,
∴E(6,7),
过E作EH⊥x轴于H,则H(6,0),
∴AH=EH=7,
∴∠EAH=45°,
过D作DF⊥x轴于F,则F(1,0),
∴BF=DF=3,
∴∠DBF=45°,
∴∠EAH=∠DBF=45°,
∴∠DBH=135°,90°<∠EBA<135°,
则点P只能在点B的左侧,有以下两种情况:
①若△DBP1∽△EAB,则![]() ,
,
∵AB=5,BD=![]() ,AE=
,AE=![]() ,
,
∴BP1=![]() =
=![]() =
=![]() ,
,
∴OP1=4-![]() =
=![]() ,
,
∴P1(![]() ,0);
,0);
②若△DBP2∽△BAE,则![]() ,
,
∵AB=5,BD=![]() ,AE=
,AE=![]() ,
,
∴BP2=![]() =
=![]() ,
,
∴OP2=![]() -4=
-4=![]() ,
,
∴P2(-![]() ,0).
,0).
综合①、②,得点P的坐标为: (![]() ,0)或 (-
,0)或 (-![]() ,0).
,0).

【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?