题目内容
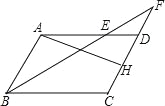
【题目】如图,在ABCD中,AB=4,AD=6,∠ABC的平分线交AD于点E,交CD的延长线于点F.
(1)求DF的长;
(2)点H为CD的中点,连接AH交BF于点G,点G是BF的中点吗?请说明理由.
【答案】(1)2.(2) 点G是BF的中点;理由见解析.
【解析】
试题分析:(1)由平行四边形的性质和角平分线证出∠F=∠FBC,得出BC=CF=6,即可得出结果;
(2)证出FH=AB,由AAS证明△ABG≌△HFG,得出对应边相等即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,BC=AD=6,CD=AB=4,
∴∠F=∠FBA,
∵∠ABC平分线为AE,
∴∠FBC=∠FBA,
∴∠F=∠FBC,
∴BC=CF=6,
∴DF=CF-CD=6-4=2.
(2)如图所示:
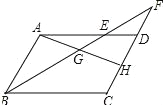
点G是BF的中点;理由如下:
∵点H为CD的中点,
∴DH=![]() CD=2,
CD=2,
∴HF=DF+HF=4,
∴HF=AB,
在△ABG和△HFG中,
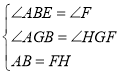 ,
,
∴△ABG≌△HFG(AAS),
∴BG=FG,
∴点G是BF的中点.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

