ЬтФПФкШн
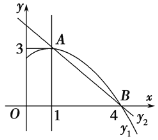
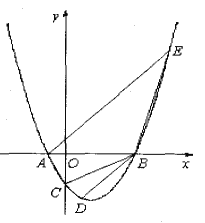
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+bx+cЃЌОЙ§ЕуBЃЈЉ4ЃЌ0ЃЉКЭЕуAЃЈ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉШЗЖЈХзЮяЯпЕФБэДяЪНЃЌВЂЧѓГіCЕузјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌХзЮяЯпЩЯДцдквЛЕуEЃЌЪЙЁїACEЪЧвдACЮЊжБНЧБпЕФжБНЧШ§НЧаЮЃЌЧѓГіЫљгаТњзуЬѕМўЕФЕуEзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌMЃЌNЪЧХзЮяЯпЩЯЕФСНЖЏЕуЃЈЕуMдкЕуЕФNзѓВрЃЉЃЌЗжБ№Й§ЕуMЃЌNзїPMЁЮxжсЃЌPNЁЮyжсЃЌPMЃЌPNНЛгкЕуPЃЎЕуMЃЌNдЫЖЏЪБЃЌЪМжеБЃГжMNЃН![]() ВЛБфЃЌЕБЁїMNPЕФСНЬѕжБНЧБпГЄГЩЖўБЖЙиЯЕЪБЃЌЧыжБНгаДГіжБЯпMNЕФБэДяЪНЃЎ
ВЛБфЃЌЕБЁїMNPЕФСНЬѕжБНЧБпГЄГЩЖўБЖЙиЯЕЪБЃЌЧыжБНгаДГіжБЯпMNЕФБэДяЪНЃЎ
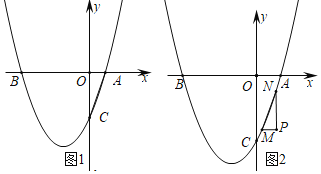
ЁОД№АИЁПЃЈ1ЃЉyЃНx2+3xЉ4ЃЌCЃЈ0ЃЌЉ4ЃЉЃЛЃЈ2ЃЉEЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђEЃЈЉ
ЃЉЛђEЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉMNЕФНтЮіЪНЮЊ
ЃЉЃЛЃЈ3ЃЉMNЕФНтЮіЪНЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)НЋЕуB(Љ4ЃЌ0)КЭЕуA(1ЃЌ0)ДњШыКЏЪ§НтЮіЪНМДПЩЧѓНтЃЛ
(2)ЗжСНжжЧщПіЃКЕБCEЁЭACЪБЃЌЩшCEЕФНтЮіЪНЮЊy=kxЉ4ЃЌЧѓГіEЕФзјБъ(kЉ3ЃЌk2Љ3kЉ4)ЃЌдйгЩЙДЙЩЖЈРэПЩЧѓkЕФжЕЃЛ![]() ЁЭACЪБЃЌдђ
ЁЭACЪБЃЌдђ![]() ЁЮCEЃЌЩш
ЁЮCEЃЌЩш![]() ЕФНтЮіЪНЮЊy=-
ЕФНтЮіЪНЮЊy=-![]() x+mЃЌМДПЩЧѓГі
x+mЃЌМДПЩЧѓГі![]() ЕузјБъЃЛ
ЕузјБъЃЛ
(3)ЗжСНжжЧщПіЃКЩшP(sЃЌt)ЃЌЕБAP=2MPЪБЃЌM(sЉ1ЃЌt)ЃЌN(sЃЌt+2)ЃЌПЩЕУ(sЉ1)2+3(sЉ1)Љ4=tЃЌs2+3sЉ4=t+2ЃЌЧѓГіs=0ЃЌt=Љ![]() ЃЌНјЖјЧѓГіM(Љ1ЃЌЉ6)ЃЌN(0ЃЌЉ4)ЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓMNЕФжБЯпНтЮіЪНЃЛЕБMP=2APЪБЃЌM(sЉ2ЃЌt)ЃЌN(sЃЌt+1)ЃЌПЩЕУ(sЉ2)2+3(sЉ2)Љ4=tЃЌs2+3sЉ4=t+1ЃЌЧѓГіs=Љ
ЃЌНјЖјЧѓГіM(Љ1ЃЌЉ6)ЃЌN(0ЃЌЉ4)ЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓMNЕФжБЯпНтЮіЪНЃЛЕБMP=2APЪБЃЌM(sЉ2ЃЌt)ЃЌN(sЃЌt+1)ЃЌПЩЕУ(sЉ2)2+3(sЉ2)Љ4=tЃЌs2+3sЉ4=t+1ЃЌЧѓГіs=Љ![]() ЃЌt=Љ
ЃЌt=Љ![]() ЃЌНјЖјЧѓГіM(Љ
ЃЌНјЖјЧѓГіM(Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌN(Љ
)ЃЌN(Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓMNЕФНтЮіЪНЃЎ
)ЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓMNЕФНтЮіЪНЃЎ
(1)ЁпЕуB(Љ4ЃЌ0)КЭЕуA(1ЃЌ0)дкХзЮяЯпЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊ(0ЃЌЉ4)ЃЛ
(2)ЕБCEЁЭACЪБЃЌ
ЩшCEЕФНтЮіЪНЮЊy=kxЉ4ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕУЃК![]() ЃЌ
ЃЌ
Ёрx=0(Щс)Лђx=kЉ3ЃЌ
ЁрЕуEЕФзјБъЮЊ(kЉ3ЃЌk2Љ3kЉ4)ЃЌ
AC2=![]() =17ЃЌ
=17ЃЌ
EA2=(kЉ3-1)2+(k2Љ3kЉ4)2ЃЌEC2=(kЉ3)2+(k2Љ3k-4+4)2ЃЌ
ЁпAC2+EC2=EA2ЃЌ
Ёр17+(kЉ3)2+(k2Љ3k)2=(kЉ4)2+(k2Љ3kЉ4)2ЃЌ
НтЕУЃКk=3(ЩсШЅ)ЃЌk=-![]() ЃЌ
ЃЌ
ЁрЕуEЕФзјБъЮЊ(Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЛ
)ЃЛ
ЕБ![]() ЁЭACЪБЃЌ
ЁЭACЪБЃЌ
ЁпCEЁЭACЃЌ
Ёр![]() ЁЮCEЃЌ
ЁЮCEЃЌ
Щш![]() ЕФНтЮіЪНЮЊy=-
ЕФНтЮіЪНЮЊy=-![]() x+mЃЌ
x+mЃЌ
ЕуA(1ЃЌ0)дкжБЯп![]() ЩЯЃЌ
ЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр ЃЌ
ЃЌ
НтЕУЃКx=1(ЩсШЅ)Лђx![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕу![]() ЕФзјБъЮЊ(Љ
ЕФзјБъЮЊ(Љ![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
злЩЯЃЌЕуEЕФзјБъЮЊ(Љ![]() ЃЌЉ
ЃЌЉ![]() )Лђ(Љ
)Лђ(Љ![]() ЃЌ
ЃЌ![]() )ЃЛ
)ЃЛ
(3)ЩшP(sЃЌt)ЃЌ
ЕБNP=2MPЪБЃЌ
ЁпMN=![]() ЃЌЧв
ЃЌЧв![]() ЃЌ
ЃЌ
ЁрMP=1ЃЌNP=2ЃЌ
ЁрM(sЉ1ЃЌt)ЃЌN(sЃЌt+2)ЃЌ
ЁпMЁЂNдкХзЮяЯпЩЯЃЌ
Ёр(sЉ1)2+3(sЉ1)Љ4=tЃЌs2+3sЉ4=t+2ЃЌ
НтЕУЃКs=0ЃЌt=Љ![]() ЃЌ
ЃЌ
ЁрM(Љ1ЃЌЉ6)ЃЌN(0ЃЌЉ4)ЃЌ
ЩшжБЯпMNЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
дђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊy=2xЉ4ЃЛ
ЕБMP=2APЪБЃЌ
ЁпMN=![]() ЃЌ
ЃЌ
ЭЌРэЃКMP=2ЃЌAP=1ЃЌ
ЁрM(sЉ2ЃЌt)ЃЌN(sЃЌt+1)ЃЌ
ЁпMЁЂNдкХзЮяЯпЩЯЃЌ
Ёр(sЉ2)2+3(sЉ2)Љ4=tЃЌs2+3sЉ4=t+1ЃЌ
Ёрs=Љ![]() ЃЌt=Љ
ЃЌt=Љ![]() ЃЌ
ЃЌ
ЁрM(Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌN(Љ
)ЃЌN(Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌ
)ЃЌ
ЩшжБЯпMNЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
дђ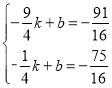 ЃЌ
ЃЌ
НтЕУЃК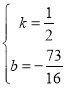 ЃЌ
ЃЌ
ЁржБЯпMNЕФНтЮіЪНЮЊy=![]() x
x![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃКMNЕФНтЮіЪНЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ