ƒøƒ⁄»ð
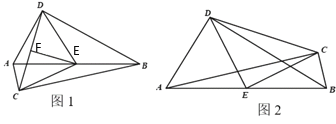
°æƒø°ø“—÷™£∫»ÁÕº£¨Rt°˜ABC∫ÕRt°˜ABD÷–£¨°œACB£Ω°œADB£Ω90°„£¨EŒ™AB÷–µ„£Æ
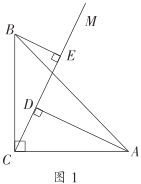
£®1£©»Ù¡Ω∏ˆ÷±Ω«»˝Ω«–Œµƒ÷±Ω«∂•µ„‘⁄ABµƒ“Ï≤ý£®»ÁÕº1£©£¨¡¨Ω”CD£¨»°CD÷–µ„F£¨¡¨Ω”EF°¢DE°¢CE£¨‘ÚDE”ÎCE ˝¡øπÿœµŒ™ £¨EF”ÎCDŒª÷√πÿœµŒ™ £ª
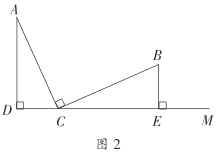
£®2£©»Ù¡Ω∏ˆ÷±Ω«»˝Ω«–Œµƒ÷±Ω«∂•µ„‘⁄ABµƒÕ¨≤ý£®»ÁÕº2£©£¨¡¨Ω”CD°¢DE°¢CE£Æ
¢Ÿ»Ù°œCAB£Ω25°„£¨°œDBA£Ω35°„£¨≈–∂œ°˜DECµƒ–Œ◊¥£¨≤¢Àµ√˜¿Ì”…£ª
¢⁄»Ù°œCAB+°œDBA£Ω![]() £¨µ±
£¨µ±![]() Œ™∂ý…Ÿ∂» ±£¨°˜DECŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨≤¢Àµ√˜¿Ì”…£Æ
Œ™∂ý…Ÿ∂» ±£¨°˜DECŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨≤¢Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©¢Ÿµ»±þ»˝Ω«–Œ£¨º˚Ω‚Œˆ£ª¢⁄45°„£¨¿Ì”…º˚Ω‚Œˆ£ª
£ª£®2£©¢Ÿµ»±þ»˝Ω«–Œ£¨º˚Ω‚Œˆ£ª¢⁄45°„£¨¿Ì”…º˚Ω‚Œˆ£ª
°æΩ‚Œˆ°ø
£®1£©∏˘æð÷±Ω«»˝Ω«–Œµƒ–±±þ÷–œþµ»”⁄–±±þµƒ“ª∞κ¥ø…µ√µΩDE=CE£¨‘Ÿ∏˘æðµ»—¸»˝Ω«–Œµƒ»˝œþ∫œ“ªµƒ–‘÷ º¥ø…µ√µΩEF°ÕCD£ª
£®2£©¢Ÿœ»∏˘æð÷±Ω«»˝Ω«–Œµƒ–‘÷ µ√µΩ°˜DEC «µ»—¸»˝Ω«–Œ£¨‘Ÿ¿˚”√Õ‚Ω«µƒ–‘÷ µ√µΩ![]() £¨
£¨![]() £¨∏˘æð∆ΩΩ«µƒ∂®“«Û≥ˆ°œDEC£¨º¥ø…µ√µΩΩ·¬€£ª
£¨∏˘æð∆ΩΩ«µƒ∂®“«Û≥ˆ°œDEC£¨º¥ø…µ√µΩΩ·¬€£ª
¢⁄”…¢Ÿµ√![]() £¨DE=EC£¨‘Ÿ∏˘æðµ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ «Û≥ˆ¥∞∏.
£¨DE=EC£¨‘Ÿ∏˘æðµ»—¸÷±Ω«»˝Ω«–Œµƒ–‘÷ «Û≥ˆ¥∞∏.
£®1£©DE=CE£¨EF°ÕCD£¨
°þ°˜ABD∫Õ°˜ABC «÷±Ω«»˝Ω«–Œ£¨°œACB£Ω°œADB£Ω90°„£¨EŒ™AB÷–µ„£¨
°ýDE=![]() AB£¨CE=
AB£¨CE=![]() AB£¨
AB£¨
°ýDE=CE£¨
°þµ„F «CDµƒ÷–µ„,
°ýEF°ÕCD£ª
£®2£©¢Ÿ°˜DECµ»±þ»˝Ω«–Œ£¨
‘⁄Rt°˜ABC∫ÕRt°˜ABD÷–£¨°œACB£Ω°œADB£Ω90°„£¨EŒ™AB÷–µ„£¨
°ý![]() £¨
£¨
°ý°˜DEC «µ»—¸»˝Ω«–Œ£¨
°þ![]() £¨
£¨![]() £¨
£¨
«“°œDEA°¢°œCEB∑÷± «°˜DEB°¢°˜AECµƒÕ‚Ω«£¨
°ý![]() £¨
£¨
![]() £¨
£¨
°ý![]() £¨
£¨
°ý°˜DEC «µ»±þ»˝Ω«–Œ£ª
¢⁄”…¢Ÿµ√DE=EC,
![]() £¨
£¨
°þ°˜DEC «µ»—¸÷±Ω«»˝Ω«–Œ£¨![]() £¨
£¨
°ý![]() £¨
£¨
°ý![]() £¨
£¨
°ýµ±![]() Œ™45∂» ±£¨°˜DECŒ™µ»—¸÷±Ω«»˝Ω«–Œ.
Œ™45∂» ±£¨°˜DECŒ™µ»—¸÷±Ω«»˝Ω«–Œ.