题目内容
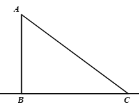
【题目】如图,在Rt△ABC中,AB=3,BC=4,AC=5,在直线BC上有P点,使△PAC是以AC为腰的等腰三角形,则BP的长为____________.
【答案】4或9或1
【解析】
分别以点A、C为等腰三角形的顶角顶点得到AP=AC、AC=PC,分别求出BP.
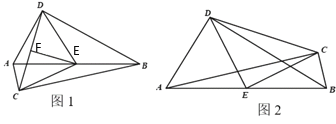
当点A为等腰三角形的顶角的顶点时,AP=AC,如图1,
∵△ABC是直角三角形,AB=3,BC=4,AC=5,
且![]() ,
,
∴∠ABP=∠ABC=90°,
∵AB=AB,AP=AC,
∴△ABP≌△ABC,
∴BP=BC=4;
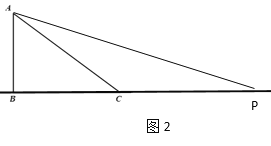
当点C为等腰三角形的顶角的顶点时,PC=AC,如图2,
则PC=AC=5,
∴BP=BC+PC=4+5=9;
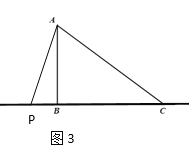
当点C为等腰三角形的顶角的顶点时,PC=AC,如图3,
则PC=AC=5,
∴BP=PC-BC=5-4=1,
综上,BP的长是4或9或1.


练习册系列答案
相关题目
【题目】甲乙两个仓库要向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨水泥,B地需110吨水泥,两库到A,B两地的路程和运费如下表(表中运费栏“元/(吨、千米)”表示每吨水泥运送1千米所需人民币)(本题满分10分)
路程/千米 | 运费(元/吨、千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A地 | 20 | 15 | 12 | 12 |
B地 | 25 | 20 | 10 | 8 |
(1)设甲库运往A地水泥![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式;
(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两地多少吨水泥时,总运费最省?最省的总运费是多少?