جâؤ؟ؤعبف
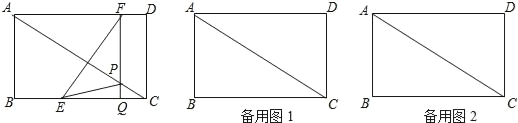
،¾جâؤ؟،؟بçح¼£¬شع¾طذخABCDضذ£¬AB=6cm£¬BC=8cm£¬بç¹ûµمEسةµمB³ِ·¢رطBC·½دٍدٍµمCشبثظشث¶¯£¬ح¬ت±µمFسةµمD³ِ·¢رطDA·½دٍدٍµمAشبثظشث¶¯£¬ثüأاµؤثظ¶ب·ض±ًخھأ؟أë2cm؛ح1cm£¬FQ،حBC£¬·ض±ً½»AC،¢BCسعµمP؛حQ£¬ةèشث¶¯ت±¼نخھtأ루0£¼t£¼4£©£®
£¨1£©ء¬½سEF£¬بôشث¶¯ت±¼نt=،، ،،ت±£¬EF،حAC£»
£¨2£©ء¬½سEP£¬µ±،÷EPCµؤأو»خھ3cm2ت±£¬اَtµؤضµ£»
£¨3£©بô،÷EQP،×،÷ADC£¬اَtµؤضµ£®
،¾´ً°¸،؟£¨1£©![]() أ룻£¨2£©2أ룻£¨3£©2أë.
أ룻£¨2£©2أ룻£¨3£©2أë.
،¾½âخِ،؟
£¨1£©دبب·¶¨³ِAC=10£¬½ّ¶ّµأ³ِ،دACBµؤسàدزضµ£¬ہûسأب½ا؛¯تµأ³ِCP£¬CG£¬¼´؟ةµأ³ِPG£¬شظإذ¶د³ِ،÷PFG،×،÷EFQ£¬½¨ء¢·½³ج¼´؟ةµأ³ِ½لآغ£¬
£¨2£©ہûسأب½اذخµؤأو»½¨ء¢·½³ج¼´؟ةµأ³ِ½لآغ£»
£¨3£©دبإذ¶د³ِEQ=CQ£¬½ّ¶ّµأ³ِCE=2CQ£¬½¨ء¢·½³ج¼´؟ةµأ³ِ½لآغ£®
½â£؛£¨1£©بçح¼1£¬
شع¾طذخABCDضذ£¬AB=6£¬BC=8£¬¸ù¾ف¹´¹ة¶¨ہيµأ£¬AC=10£¬
،ك،دB=،دD=،دBCD=90،م£¬FQ،حBCسعQ£¬
،àثؤ±كذخCDFQتا¾طذخ£¬
،àCQ=DF£¬
سةشث¶¯ضھ£¬BE=2t£¬DF=t£¬
،àCQ=t£¬CE=BC©پBE=8©پ2t£¬AF=8©پt£¬
،àEQ=CE©پCQ=8©پ3t£¬
شعRt،÷ABCضذ£¬cos،دACB=![]() £¬
£¬
شعRt،÷CPQضذ£¬cos،دACB=![]() ,
,
،àCP=![]() t£¬
t£¬
،كEF،حAC£¬
،à،دCGE=90،م=،دABC£¬
،à،دACB+،دFEQ=90،م£¬
،ك،دACB+،دBAC=90،م£¬
،à،دFEQ=،دBAC£¬
،à،÷ABC،×،÷EQF£®
،à![]()
،à![]() £¬
£¬
،àEQ=![]() £¬
£¬
،à8©پ3t=![]() £¬
£¬
t=![]() أ룻
أ룻
¹ت´ً°¸تا£؛![]() أ룻
أ룻
£¨2£©سة£¨1£©ضھ£¬CE=8©پ2t£¬CQ=t£¬
شعRt،÷ABCضذ£¬tan،دACB=![]() £¬
£¬
شعRt،÷CPQضذ£¬tan،دACB=![]() £¬
£¬
،àPQ=![]() t£¬
t£¬
،ك،÷EPCµؤأو»خھ3cm2£¬
،àS،÷EPC=![]() CE،ءPQ=
CE،ءPQ=![]() ،ء£¨8©پ2t£©،ء
،ء£¨8©پ2t£©،ء![]() t=3£¬
t=3£¬
،àt=2أ룬
¼´£؛tµؤضµخھ2أ룻
£¨3£©ثؤ±كذخABCDتا¾طذخ£¬
،àAD،خBC£¬
،à،دCAD=،دACB£¬
،ك،÷EQP،×،÷ADC£¬
،à،دCAD=،دQEP£¬
،à،دACB=،دQEP£¬
،àEQ=CQ£¬
،àCE=2CQ£¬
سة£¨1£©ضھ£¬CQ=t£¬CE=8©پ2t£¬
،à8©پ2t=2t£¬
،àt=2أ룮
¼´£؛tµؤضµخھ2أ룮

 ذآ»îء¦×ـ¶¯ش±تîدµءذ´ً°¸
ذآ»îء¦×ـ¶¯ش±تîدµءذ´ً°¸ ءْبثح¼تé؟ىہض¼ظئعتî¼ظ×÷زµض£ضف´َر§³ِ°وةçدµءذ´ً°¸
ءْبثح¼تé؟ىہض¼ظئعتî¼ظ×÷زµض£ضف´َر§³ِ°وةçدµءذ´ً°¸