题目内容
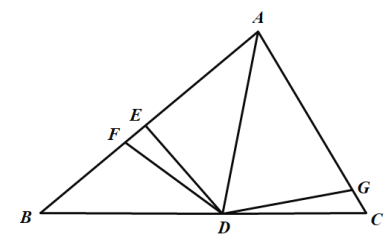
【题目】如图,在![]() 中,
中,![]() 为
为![]() 边上的中点.
边上的中点.
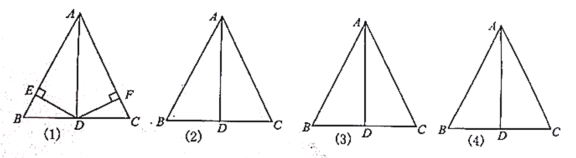
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .判断
.判断![]() 的形状,并证明;
的形状,并证明;
(2)若![]() 分别是
分别是![]() 上的中线,连接
上的中线,连接![]() .判断
.判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 分别是
分别是![]() 的平分线,连接
的平分线,连接![]() .判断
.判断![]() 的关系,不需证明;
的关系,不需证明;
(4)若分别在![]() 上任取一点
上任取一点![]() ,且
,且![]() ,连接
,连接![]() .在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
.在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
【答案】(1)![]() 是等腰三角形,理由见解析;(2)
是等腰三角形,理由见解析;(2)![]() 是等腰三角形,理由见解析;(3)
是等腰三角形,理由见解析;(3)![]() 且
且![]() ;(4)
;(4)![]() 是等腰三角形,
是等腰三角形,![]() 是EF的垂直平分线,
是EF的垂直平分线,![]() ,
,![]() .
.
【解析】
(1)依据等腰三角形三线合一的性质,及角平分线的性质,可以证明![]() 是等腰三角形;
是等腰三角形;
(2)由![]() 分别是
分别是![]() 上的中线,
上的中线,![]() ,得
,得![]() ,依据SAS证明
,依据SAS证明![]() ≌
≌![]() ,从而
,从而![]() ,即证明
,即证明![]() 是等腰三角形;
是等腰三角形;
(3)![]() 分别是
分别是![]() 的平分线,结合三线合一中AD是高,可得
的平分线,结合三线合一中AD是高,可得![]() ,从而
,从而![]() 即
即![]() ,
,![]() ≌
≌![]() (ASA),依据全等的性质得
(ASA),依据全等的性质得![]() ,所以
,所以![]() 且
且![]() ;
;
(4)依据轴对称的知识即可作答.
(1)![]() 是等腰三角形,理由如下:
是等腰三角形,理由如下:

∵在![]() 中,
中,![]() 为
为![]() 边上的中点,
边上的中点,
∴![]() 是平分
是平分![]() ,
,
又∵![]() ,
,![]() ,
,
![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(2)![]() 是等腰三角形,理由如下:
是等腰三角形,理由如下:

∵![]() 分别是
分别是![]() 上的中线,
上的中线,![]()
∴![]() ,
,
又∵由![]() 是平分
是平分![]() 得
得![]() ,
,
![]() ,
,
∴![]() ≌
≌![]() (SAS),
(SAS),
∴![]() ,
,
∴![]() 是等腰三角形;
是等腰三角形;
(3)![]() .
.

(4)![]() 是等腰三角形,
是等腰三角形,![]() 是EF的垂直平分线,
是EF的垂直平分线,![]() ,
,![]() .(答案不唯一,依据轴对称回答即可).
.(答案不唯一,依据轴对称回答即可).

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目