题目内容
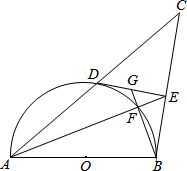
如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,AE=
(1)求
的长;
(2)若AD=
+5,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.

| 3 |
(1)求
 |
| EF |
(2)若AD=
| 3 |

(1)连接OE、OF,
∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,
∴∠A=90°,∠OEA=∠OFA=90°
∴四边形AFOE是正方形
∴∠EOF=90°,OE=AE=
∴
的长=
=
π.
(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,
连接OM1、OR,
∵M1N1∥MN
∴∠DM1N1=∠DMN=60°
∴∠EM1N1=120°
∵MA、M1N1切⊙O于点E、R
∴∠EM1O=
∠EM1N1=60°
在Rt△EM1O中,EM1=
=
=1
∴DM1=AD-AE-EM1=
+5-
-1=4.
过点D作DK⊥M1N1于K
在Rt△DM1K中
DK=DM1×sin∠DM1K=4×sin∠60°=2
即d=2
,
∴当d=2
时,直线MN与⊙O相切,
当1≤d<2
时,直线MN与⊙O相离,
当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2
+
=3
>4,
∴当2
<d≤4时,MN直线与⊙O相交.

∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,
∴∠A=90°,∠OEA=∠OFA=90°
∴四边形AFOE是正方形
∴∠EOF=90°,OE=AE=
| 3 |
∴
 |
| EF |
90π×
| ||
| 180 |
| ||
| 2 |
(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,
连接OM1、OR,
∵M1N1∥MN
∴∠DM1N1=∠DMN=60°
∴∠EM1N1=120°

∵MA、M1N1切⊙O于点E、R
∴∠EM1O=
| 1 |
| 2 |
在Rt△EM1O中,EM1=
| OE |
| tan∠EM1O |
| ||
| tan60° |
∴DM1=AD-AE-EM1=
| 3 |
| 3 |
过点D作DK⊥M1N1于K
在Rt△DM1K中
DK=DM1×sin∠DM1K=4×sin∠60°=2
| 3 |
| 3 |
∴当d=2
| 3 |
当1≤d<2
| 3 |
当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2
| 3 |
| 3 |
| 3 |
∴当2
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



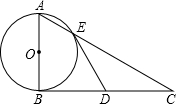
 =4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是______cm.
=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是______cm.
