题目内容
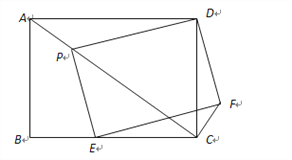
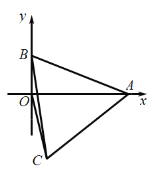
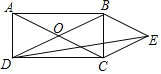
【题目】如图，矩形ABCD的对角线AC、BD相交于点O，AB：BC＝2：1，且BE∥AC，CE∥DB，连接DE，则tan∠EDC＝（ ）
A.
B.
C.
D.
【答案】D
【解析】
过点E作
，连接OE交BC于点G，根据邻边相等的平行四边形是菱形即可判断四边形OBEC是菱形，则OE与BC垂直平分，易得
，CF=x，再由锐角三角函数定义作答．
∵矩形ABCD的对角线AC、BD相较于点O，AB：BC＝2：1，
∴BC=AD，
设AB=2x，则BC=x，
如图，过点E作，交线段DC的延长线于点F，连接OE交BC于点G，
∵
，
，
∴四边形BOCE是平行四边形，
∵四边形ABCD是矩形，
∴OB=OC，
∴四边形BOCE是菱形，
∴OE与BC垂直平分，
∴
，
，
∴四边形AOEB是平行四边形，
∴OE=AB=2x，
∴
，
∴
．
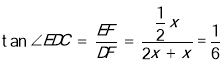故答案选D．
练习册系列答案
相关题目
