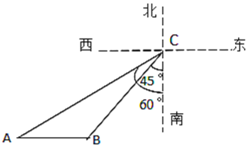
ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚÄ³ŗ£Óņ£¬Ņ»ĖŅÖø»Ó“¬ŌŚ![]() “¦ŹÕµ½ÓꓬŌŚ
“¦ŹÕµ½ÓꓬŌŚ![]() “¦·¢³öµÄĒó¾ČŠÅŗÅ£¬¾Č·¶Ø£¬ÓöĻÕÅ×ĆŖµÄÓꓬĖłŌŚµÄ
“¦·¢³öµÄĒó¾ČŠÅŗÅ£¬¾Č·¶Ø£¬ÓöĻÕÅ×ĆŖµÄÓꓬĖłŌŚµÄ![]() “¦Ī»ÓŚ
“¦Ī»ÓŚ![]() “¦µÄÄĻĘ«Ī÷45”ć·½ĻņÉĻ£¬ĒŅ
“¦µÄÄĻĘ«Ī÷45”ć·½ĻņÉĻ£¬ĒŅ![]() ŗ£Ąļ£»Öø»Ó“¬ĖŃĖ÷·¢ĻÖ£¬ŌŚ
ŗ£Ąļ£»Öø»Ó“¬ĖŃĖ÷·¢ĻÖ£¬ŌŚ![]() “¦µÄÄĻĘ«Ī÷60”ć·½ĻņÉĻÓŠŅ»ĖŅŗ£¼ą“¬
“¦µÄÄĻĘ«Ī÷60”ć·½ĻņÉĻÓŠŅ»ĖŅŗ£¼ą“¬![]() £¬Ē”ŗĆĪ»ÓŚ
£¬Ē”ŗĆĪ»ÓŚ![]() “¦µÄÕżĪ÷·½Ļņ£®ÓŚŹĒĆüĮīŗ£¼ą“¬
“¦µÄÕżĪ÷·½Ļņ£®ÓŚŹĒĆüĮīŗ£¼ą“¬![]() Ē°ĶłĖŃ¾Č£¬ŅŃÖŖŗ£¼ą“¬
Ē°ĶłĖŃ¾Č£¬ŅŃÖŖŗ£¼ą“¬![]() µÄŗ½ŠŠĖŁ¶ČĪŖ30ŗ£Ąļ/Š”Ź±£¬ĪŹÓꓬŌŚ
µÄŗ½ŠŠĖŁ¶ČĪŖ30ŗ£Ąļ/Š”Ź±£¬ĪŹÓꓬŌŚ![]() “¦ŠčŅŖµČ“ż¶ą³¤Ź±¼ä²ÅÄܵƵ½ŗ£¼ą“¬
“¦ŠčŅŖµČ“ż¶ą³¤Ź±¼ä²ÅÄܵƵ½ŗ£¼ą“¬![]() µÄ¾ČŌ®£æ£Ø²Īæ¼Źż¾Ż£ŗ
µÄ¾ČŌ®£æ£Ø²Īæ¼Źż¾Ż£ŗ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ½į¹ū¾«Č·µ½0.1Š”Ź±£©
½į¹ū¾«Č·µ½0.1Š”Ź±£©
”¾“š°ø”æ1.4Š”Ź±
”¾½āĪö”æ
ŃÓ³¤AB½»ÄĻ±±ÖįÓŚµćD£¬ŌņAB”ĶCDÓŚµćD£¬Ķعż½āÖ±½ĒČż½ĒŠĪBDCŗĶADC£¬Ēó³öBD”¢CDŗĶADµÄ³¤£¬¼Ģ¶ųĒó³öABµÄ³¤£¬“Ó¶ųæÉŅŌ½ā¾öĪŹĢā.
½ā£ŗŅņĪŖAŌŚBµÄÕżĪ÷·½£¬ŃÓ³¤AB½»ÄĻ±±ÖįÓŚµćD£¬ŌņAB”ĶCDÓŚµćD
”ß”ĻBCD=45”ć£¬BD”ĶCD
”ąBD=CD
ŌŚRt”÷BDCÖŠ£¬”ß![]() £¬BC=80ŗ£Ąļ
£¬BC=80ŗ£Ąļ
¼“![]() £¬½āµĆ
£¬½āµĆ![]() ŗ£Ąļ
ŗ£Ąļ
”ą![]() ŗ£Ąļ
ŗ£Ąļ
ŌŚRt”÷ADCÖŠ£¬”ß![]()
¼“![]() £¬½āµĆ
£¬½āµĆ![]() ŗ£Ąļ
ŗ£Ąļ
”ßAB=AD£BD
”ą![]() ŗ£Ąļ
ŗ£Ąļ
”ąÓꓬŌŚB“¦ŠčŅŖµČ“żµÄŹ±¼äĪŖ![]() Š”Ź±
Š”Ź±
”ąÓꓬŌŚB“¦“óŌ¼ŠčµČ“ż1.4Š”Ź±.


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æĪŖŠū“«6ŌĀ6ČÕŹĄ½ēŗ£ŃóČÕ£¬Ä³Š£¾ÅÄź¼¶¾ŁŠŠĮĖÖ÷ĢāĪŖ”°ÕäĻ§ŗ£Ńó׏Ō“£¬±£»¤ŗ£ŃóÉśĪļ¶ąŃłŠŌ”±µÄÖŖŹ¶¾ŗČü»ī¶Æ£®ĪŖĮĖ½āČ«Äź¼¶500Ćūѧɜ“Ė“Ī¾ŗČü³É¼ØµÄĒéæö£¬Ė껜³éČ”ĮĖ²æ·Ö²ĪČüѧɜµÄ³É¼Ø£¬ÕūĄķ²¢»ęÖĘ³öČēĻĀ²»ĶźÕūµÄĶ³¼Ę±ķŗĶĶ³¼ĘĶ¼£ØČēĶ¼£©£®Ēėøł¾ŻĶ¼±ķŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
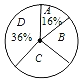
ÖŖŹ¶¾ŗČü³É¼Ø·Ö×éĶ³¼Ę±ķ
×鱚 | ·ÖŹż/·Ö | ʵŹż |
A | 60”Üx£¼70 | a |
B | 70”Üx£¼80 | 10 |
C | 80”Üx£¼90 | 14 |
D | 90ӆxӆ100 | 18 |
£Ø1£©±¾“Īµ÷²éŅ»¹²Ė껜³éČ”ĮĖ”” ””Ćū²ĪČüѧɜµÄ³É¼Ø£»
£Ø2£©±ķ1ÖŠa£½”” ””£»
£Ø3£©Ėł³éČ”µÄ²ĪČüѧɜµÄ³É¼ØµÄÖŠĪ»ŹżĀäŌŚµÄ”°×鱚”±ŹĒ”” ””£»
£Ø4£©ĒėÄć¹Ą¼Ę£¬øĆŠ£¾ÅÄź¼¶¾ŗČü³É¼Ø“ļµ½80·ÖŅŌÉĻ£Øŗ¬80·Ö£©µÄѧɜŌ¼ÓŠ”” ””ČĖ£®