题目内容
【题目】如图,抛物线![]() 经过点A(4,0)、B(1,0),交y轴于点C.
经过点A(4,0)、B(1,0),交y轴于点C.
(1)求抛物线的解析式.
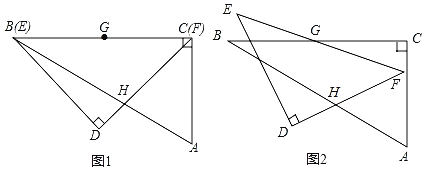
(2)点P是直线AC上方的抛物线上一点,过点P作![]() 于点H,求线段PH长度的最大值.
于点H,求线段PH长度的最大值.
(3)Q为抛物线上的一个动点(不与点A、B、C重合),![]() 轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
轴于点M,是否存在点Q,使得以点A、Q、M三点为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标,若不存在,请说明理由.
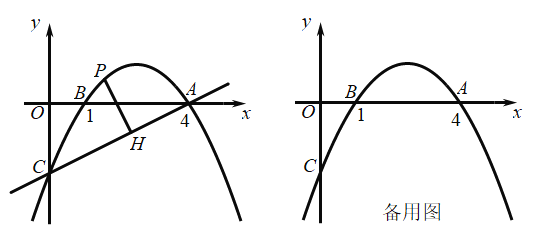
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)根据待定系数法解答即可;
(2)先利用待定系数法求出直线AC的解析式,过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,设点P的横坐标为t,则PE可用含t的代数式表示,易证△PEH∽△ACO,可得![]() ,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
,于是PH可用含t的代数式表示,然后根据二次函数的性质即可求出PH长度的最大值;
(3)设Q点的横坐标为m,则Q点的纵坐标可用m的代数式表示,分三种情况:当1<m<4时,如图2;当m>4时,如图3;当m<1时,如图4,根据相似三角形的性质分![]() 与
与![]() 两种情况,建立关于m的方程求解即可.
两种情况,建立关于m的方程求解即可.
解:(1)将 A(4,0)、B(1,0)代入![]() ,
,
得:![]() ,解得
,解得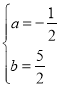 ,
,
∴抛物线的解析式为![]() ;
;
(2)将![]() 代入
代入![]() ,得
,得![]() ,∴
,∴![]() .
.
设直线 AC 的解析式为![]() ,
,
将 A(4,0)代入![]() ,解得:
,解得:![]() ,
,
∴直线 AC 的解析式为![]() .
.
过点 P 作 x 轴的垂线,交直线 AC 于点 E,如图1,
设 ![]() ,则
,则![]() .
.
∴![]() .
.
∵∠PEH=∠ACO,∠PHE=∠AOC=90°,
∴△PEH∽△ACO,
∴![]() ,
,
∴![]() .
.
∴当![]() 时,PH 有最大值
时,PH 有最大值![]() ;
;
(3)存在,点![]() 或
或![]() 或
或![]() .
.
理由如下:
设Q点的横坐标为m,则Q点的纵坐标为﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
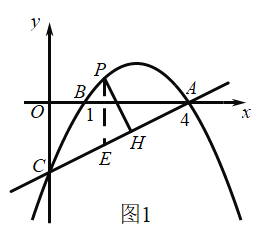
当1<m<4时,如图2,AM=4﹣m,QM=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即4﹣m=2(﹣
时,△AQM∽△ACO,即4﹣m=2(﹣![]() m2+
m2+![]() m﹣2),
m﹣2),
解得:m=2或m=4(舍去),
此时Q(2,1);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=﹣
时,△AQM∽△CAO,即2(4﹣m)=﹣![]() m2+
m2+![]() m﹣2,
m﹣2,
解得:m=4或m=5(均不合题意,舍去);
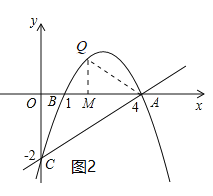
当m>4时,如图3,AM=m-4,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
∴①当![]() 时,△AQM∽△ACO,即m-4=2(
时,△AQM∽△ACO,即m-4=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=2或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(m-4)=
时,△AQM∽△CAO,即2(m-4)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=5或m=4(不合题意,舍去);
∴Q(5,﹣2);
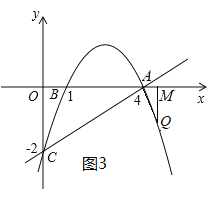
当m<1时,如图4,AM=4-m,QM=![]() m2-
m2-![]() m+2,
m+2,
又∵∠COA=∠QMA=90°,
①当![]() 时,△AQM∽△ACO,即4﹣m=2(
时,△AQM∽△ACO,即4﹣m=2(![]() m2-
m2-![]() m+2),
m+2),
解得:m=0或m=4(均不合题意,舍去);
②当![]() 时,△AQM∽△CAO,即2(4﹣m)=
时,△AQM∽△CAO,即2(4﹣m)=![]() m2-
m2-![]() m+2,
m+2,
解得:m=﹣3或m=4(不合题意,舍去);
∴Q(﹣3,﹣14);
综上所述,符合条件的点Q为(2,1)或(5,﹣2)或(﹣3,﹣14).

【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图).请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A | 60≤x<70 | a |
B | 70≤x<80 | 10 |
C | 80≤x<90 | 14 |
D | 90≤x≤100 | 18 |
(1)本次调查一共随机抽取了 名参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.