题目内容
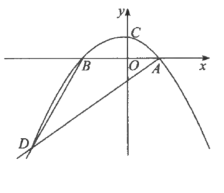
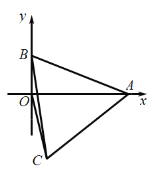
【题目】如图，在直角坐标系中，已知点A(6，0)，点B为y轴正半轴上一动点，连接AB，以AB为一边向下作等边△ABC，连接OC，则OC的最小值（ ）
A.
B.
C.
D.
【答案】B
【解析】
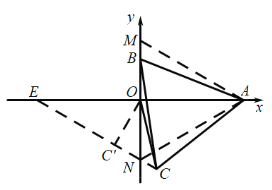
以OA为对称轴作等边△AMN，由“SAS”可证△ANC≌△AMB，可得∠AMB=∠ANC=60°，由直角三角形的性质可求∠AEN=30°，EO= 
ON=6，则点C在EN上移动，当OC'⊥EN时，OC'有最小值，即可求解．
解：如图，以OA为对称轴作等边△AMN，延长CN交x轴于E，
∵△ABC是等边三角形，△AMN是等边三角形，
∴AM=AN，AB=AC，∠MAN=∠BAC，∠AMN=60°=∠ANM， ∴∠BAM=∠CAN，
∴△ANC≌△AMB（SAS），
∴∠AMB=∠ANC=60°，
∴∠ENO=60°，
∵AO=6，∠AMB=60°，AO⊥BO，
∴MO=NO=
∵∠ENO=60°，∠EON=90°，
∴∠AEN=30°，EO=ON=6，
∴点C在EN上移动，
∴当OC'⊥EN时，OC'有最小值，
此时，O'C=
EO=3，
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
