题目内容
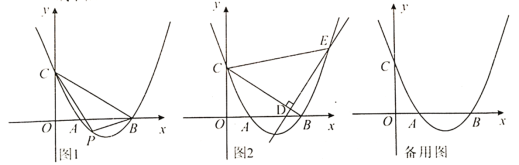
【题目】反比例函数![]() 的函数图象经过
的函数图象经过![]() 两点,过
两点,过![]() 两点作一直线.
两点作一直线.
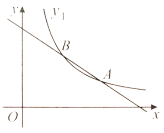
(1)求反比例函数解析式;
(2)将反比例函数![]() 向下平移1个单位,得函数
向下平移1个单位,得函数![]() ________;函数
________;函数![]() 与坐标轴的交点为__________;
与坐标轴的交点为__________;
(3)将直线![]() 向下平移
向下平移![]() 个单位后与函数
个单位后与函数![]() 的图象有唯一交点,求
的图象有唯一交点,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)将点A和点B的坐标代入反比例函数解析式中即可求出结论;
(2)根据函数的平移规律即可求出函数![]() ,然后根据坐标轴上点的坐标规律代入解析式即可求出结论;
,然后根据坐标轴上点的坐标规律代入解析式即可求出结论;
(3)先利用待定系数法求出直线AB的解析式,即可表示出直线![]() 平移后的解析式,然后联立方程,根据题意,令联立后一元二次方程的
平移后的解析式,然后联立方程,根据题意,令联立后一元二次方程的![]() 即可求出结论.
即可求出结论.
解:(1)![]() 反比例函数
反比例函数![]() 经过
经过![]() 两点,
两点,
![]() ,
,
解得:![]() ,
,
![]() 反比例函数解析式为
反比例函数解析式为![]()
(2)将反比例函数![]() 向下平移1个单位,得函数
向下平移1个单位,得函数![]() ,
,
![]()
![]() 函数
函数![]() 与
与![]() 轴无交点,
轴无交点,
将![]() 代入得
代入得![]() ,
,
![]()
![]() 与
与![]() 轴得交点为
轴得交点为![]()
故答案:![]() ;
;![]() .
.
(3)设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入解析式中,得
代入解析式中,得
![]()
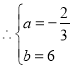
![]() 直线
直线![]() 的解析式为
的解析式为![]()
设平移后的解析式为![]() ,
,
联立方程组得: ,
,
整理得:
![]() ,若两函数图象有唯一交点,
,若两函数图象有唯一交点,
则![]()
解得:![]() ,
,![]() ,
,
当![]() 时,
时,![]()
解得:![]() (不符合x的取值范围)
(不符合x的取值范围)
∴![]() 舍去;
舍去;
当![]() 时,
时,![]()
解得:![]()
故![]() 的值为
的值为![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目