题目内容
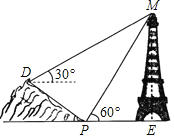
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=![]() ,请你帮助小明计算古塔的高度ME.(结果保留根号)
,请你帮助小明计算古塔的高度ME.(结果保留根号)
【答案】古塔的高度ME约为(22.5+10![]() )m.
)m.
【解析】
作DC⊥EP交EP的延长线于C,作DF⊥ME于F,作PH⊥DF于H,然后根据坡度的定义分别求出DC,再根据勾股定理的出CP,设![]() ,根据正切的定义用y分别表示DF、PE,再根据题意列方程求解即可得出答案.
,根据正切的定义用y分别表示DF、PE,再根据题意列方程求解即可得出答案.
解:作DC⊥EP交EP的延长线于C,作DF⊥ME于F,作PH⊥DF于H,
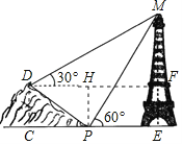
则DC=PH=FE,DH=CP,HF=PE,
设![]() ,
,
∵![]() ,
,
∴![]() ,
,
由勾股定理得,PD2=DC2+CP2,即252=(3x)2+(4x)2,
解得,x=5,
则DC=3x=15,CP=4x=20,
∴DH=CP=20,PH=FE=DC=15,
设![]() ,
,
则![]() m,
m,
在![]() 中,
中,![]() ,
,
则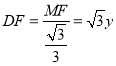 ,
,
在![]() 中,
中,![]() ,
,
则PE=![]() =
=![]() ,
,
∵DH=DF﹣HF,
∴![]() ,
,
解得,![]() ,
,
∴![]()
答:古塔的高度ME约为(![]() )m.
)m.

练习册系列答案
相关题目