题目内容
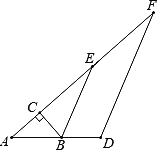
【题目】如图,已知:∠AOB=90°,OE是∠AOB的平分线,P是OE上一动点,PC⊥PD,C、D分别在OA、OB上.求证:PC=PD.

【答案】见解析.
【解析】
过点P作PM⊥OA于点M,PN⊥OB于点N,
根据垂直的定义得到∠PMC=∠PND=90°,
根据角平分线的性质得到PE=PF,
利用四边形内角和定理得到∠PCM+∠PDO=360°-90°-90°=180°,
而∠PDO+∠PDN=180°,则∠PCM=∠PDN,
然后根据AAS可判断△PCM≌△PDN,
根据全等的性质即可得到PC=PD.
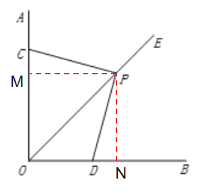
证明:过点P作PM⊥OA于点M,PN⊥OB于点N,如图
∴∠PMC=∠PND=90°
∵OE是∠AOB的平分线
∴PM=PN
∵∠AOB=90°,∠CPD=90°
∴∠PCM+∠PDO=360°-90°-90°=180°
而∠PDO+∠PDN=180°
∴∠PCM=∠PDN
在△PCM和△PDN中
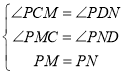
∴△PCM≌△PDN(AAS)
∴PC=PD

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目